 Rob Kremer
Rob Kremer

 Chapter 8
Chapter 8
 index
index
 References
References
This chapter evaluates the Constraint Graphs framework and describes several potential areas of future work in the field. The evaluation addresses the objectives described in chapters 1 and 4, and describes how these objectives are met by the research work. The evaluation also discusses several issues related to the framework's efficiency, scalability, expressiveness, completeness, extendibility, and flexibility.
In addition to the evaluation, this chapter describes several avenues of future research based on the current work. The current theory should be challenged based on the implementation of other existing and newly designed concept mapping languages. There are also many possible alternative and variant theories that warrant investigation using variants of the software framework described in this thesis. It now seems apparent that the framework and theory could be easily and profitably extended to implement not just the syntax (Section 7.2), but all the semantics of Conceptual Graphs. Translators similar to the Z translator described in Section 7.3 could be used to link to other server programs to create systems that encompass both interactive syntax support (Constraint Graphs) and the "deep semantics" support of a language-specific (but non-graphical) server. A Java version of the CMap user interface could be used to increase Constraint Graphs portability to other environments. In addition, there are many avenues of research to pursue in order to make Constraint Graphs a powerful multi-user, collaborative tool.
The primary objective of this work was stated in chapter 1:
"to provide the basis for concrete theories of concept mapping language syntax by developing a software framework for the development and implementation of concept mapping languages."
Two auxiliary objectives were derived from this: formal specification and disciplined development. The formal specification objective comes from the need for unambiguous description, since Constraint Graphs can support no theory if they are not unambiguously understood. The disciplined development objective comes from the need to have confidence in the correspondence between the specification and the program.
The requirements for the framework (which constitute a commitment to a minimal theory of concept mapping languages) were developed in chapter 4. From these requirements the specification was developed in chapter 5. While the specification does not cover the whole of the framework software, it does cover the essential part that implements the corresponding theory of concept maps. This includes the fundamental component types of a concept map: nodes, contexts, arcs, and the inheritance mechanism, isa arcs. The specification unambiguously documents:
This specification, given in chapter 5, fulfills the formal specification auxiliary objective.
Chapter 6 describes an implementation of the framework software. Although the software is written in a very different language (C++) from the specification (Z), the implementation is carefully structured to follow the specification as closely as possible. Unfortunately, following the Z specification's exact structure yields an implementation far too slow for practical purposes. This problem forced the implementation to cache the isa arc references, which was a slight divergence from the structure of the specification. Fortunately, taking only this shortcut was enough to increase the speed an average of two or three orders of magnitude (the computational complexity of the subtype calculation was reduced from fourth-order polynomial to almost linear). The vast majority of the implementation closely follows the specification structure. Both specification and implementation have been annotated with HTML anchor tags such that their trivial conversion to HTML documents allows two-way hyperlinks between the parts of the specification and the corresponding parts of the implementation.
However, there is an efficiency cost associated with maintaining the close correspondence between specification and implementation (see Section 6.5.3). Reducing this correspondence could significantly reduce the overall computational complexity, and may be necessary in the future as the framework is applied to larger data sets or is extended to different kinds of constraints.
In addition, chapter 6 describes the conceptual framework used in the design and implementation to make the program more understandable and high-level. Gamma's design patterns (Gamma et al. 1995) are high level organizational descriptions used in the design of the software. The C++ Standard Template Library (Nelson 1995; Stepanov & Lee 1995) is a very abstract and type-safe container library that was used in the implementation to avoid "reinventing the wheel" and offer a direct higher level of abstraction in the programming language.
The implementation has an (almost) direct correspondence to the specification. It also makes use of high-level conceptual frameworks in design and implementation. This disciplined approach yields an acceptable level of confidence that the implementation is a reasonable "concrete" facsimile of the specification.
Chapter 7 serves as a test of the primary objective of this work: to develop a software framework for the implementation of concept mapping languages. Chapter 7 describes, in detail, three concept mapping languages implemented in the Constraint Graphs framework. These languages vary in complexity from the simple gIBIS, a decision support language, to Conceptual Graphs and KDraw, both knowledge representation languages. The implementation of the syntax (and some of the semantics) of these three languages demonstrates Constraint Graphs' fulfillment of the primary objective of the thesis. This should not be taken as a claim that the theory will encompass all languages that one might want to include in the class of concept mapping languages: that will only come with further experience implementing more languages under the framework.
This section discusses the efficiency and scalability, expressiveness and completeness, extendibility, and flexibility of the current framework implementation. Most of the points within these areas are discussed elsewhere in this thesis; these are noted in the discussion.
As has already been addressed in Section 9.1, efficiency is one of Constraint Graphs' concerns with respect to scaling up to large data sets. Efficiency has been purposefully sacrificed in favour of achieving a clean correspondence between the implementation code and the specification. However, the correspondence has been compromised because the early implementations proved much too slow. This forced references to isa arcs to be locally cached within component objects. In fact, the implementation maintains both the cached and uncached strategies by use of conditional compilation. The compilation is dependent on whether or not the macro symbol FAST1 is defined, as seen in the following code excerpt of the declaration of the Component0 class (the superclass of all component classes):
class Component0 : public Subject //inherit for the Observer/Subject pattern
#ifdef FAST1
,public Observer
#endif
{
friend class TypedGraph;
public:
typedef set<Ref2<Attribute>,less<Attribute> > PolySetOfAttributes;
typedef PolySetOfAttributes::iterator AttrIterator;
#ifdef FAST1
typedef list<IsaComponent*> Isas_type;
typedef Isas_type::iterator IsaIterator;
#endif
...
protected:
ID_type Id;
string Name;
unsigned int Level;
PolySetOfAttributes Attributes;
#ifdef FAST1
Isas_type ParentIsas;
Isas_type ChildIsas;
#endif
};
Here, the Observerclass is a superclass of
Component0only if this is a cached compilation. Likewise, the two lists
of cached isa references and their relevant typedefs are
only declared in a cached compilation. This measure allows for
checking the cached version against the original uncached version
during testing, and increases confidence in the equivalence of
the specification and implementation. Section 6.5.3 discusses
more technical details on cache optimization.As Constraint Graphs is applied against larger and larger data sets in future work, it will undoubtedly show performance problems. The caching of other (non-isa) arc references are obvious candidates for efficiency improvements. Other efficiency strategies include:
The design of Constraint Graphs concentrates on arcs and which node types they may terminate on. A corollary of that is the attention to the type lattice and the subtype/supertype relationship, since typing is the basis of arc constraints. Complex arc constraints, based on more information than just the type of the arc and the type of the termination node, are not supported except by ad-hoc constraints. An example of a complex constraint might be the modeling of sex in type Person by attribute instead of by subtyping:
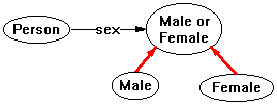
When modeled this way, the relationship mother is restricted to being from a Person to a Person whose sex relation terminates on Female, which could be drawn this way:
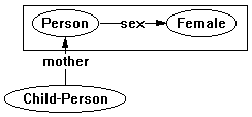
where the context box indicates the secondary restriction on the Person at the terminal of the mother relationship. Allowing this kind of specification can lead to arbitrarily complex structures, which leads to very high computational complexity in the constraint validation algorithm. Since this sort of specification appears to be fairly unusual (although it's hard to tell how much it would be used if it were readily available), it does not seem worth the additional complexity at this time - particularly since ad-hoc constraints can be used for the (apparently) rare cases where complex arc constraints are required.
Contexts have been specified as being hierarchical (nested) in Constraint Graphs. But there is no inherent reason why concept mapping languages need only hierarchical contexts: overlapping contexts are also possible (and more general). However, the author knows of no concept mapping language that allows overlapping contexts (few even allow contexts), but there are other graphical languages (Venn diagrams (Hammer 1995), for instance) that do allow overlapping contexts. While there is no current compelling reason to allow overlapping contexts, it may be necessary to roll back this commitment in the future. Fortunately, this would be easy: the nested contexts restriction is implemented as a simple ad-hoc constraint (Sections 5.6, 5.8, and 5.10), and could be removed or replaced by some other appropriate constraint. Even an end-user could remove the constraint, since it's a simple matter of removing it from the ContextComponents's "constraints" attribute: there is no programming involved.
Contexts are also problematic in another way: there is no obvious "right" way for context boxes to behave in the user interface. Currently, moving a context box moves all the components it contains as well as includes all components its post-operation geometry happens to contain. Resizing a context box includes (or excludes) all the components the post-operation geometry includes (or excludes). But there are compelling alternatives. Moving a context box could move all the contained components and "bump" all the components from its new location to maintain its containment state. Resizing a context box could compress all contained components or "bump" all excluded components to maintain its original containment state.
Besides the expected extendibility that comes with the object oriented programming paradigm, Constraint Graphs is easily extendible in at least three respects:
Ad-hoc constraints are implemented as instances of the abstract class Validator. Arbitrary constraints may be easily added to the system by sub-classing Validator and adding an instance of the new class to the global constraint library. (Since Validator is clonable, the system can produce exact-typed copies of a specific Validator subclass without knowing the specific type - see Section 6.5.2.) The system calls the bool operator() method to check for pass/fail status of the validator. The system does not have to worry about details of the validators: it merely keeps lists of validators and applies them as necessary in its validation algorithm (see Section 6.4.3). Thus, it is relatively easy to extend the system using validators with very minimal disruption to the program code.
Validators are stored in attribute/value pairs, as are all of the visual attributes (such as shape, fill color, and text color) used in the user interface. Attribute/value pairs are type-safe, identifier-indexable places where other programs or modules can easily store inheritable data within a Constraint Graphs concept map. This allows, for instance, the CMap user interface to store data (of which Constraint Graphs has no semantic knowledge) in a concept map; that data can be accessed later, or used concurrently by other views using the same concept map (see Section 6.1). Attributes and their values are also automatically inherited by subtypes of the component in which they are stored.
The library pattern, discussed in Section 6.5.2, allows for the easy extension of constraints and various graphical object types.
These three features, ad-hoc constraints, attribute/value pairs, and the library pattern, along with object-oriented design and implementation, combine to make the Constraint Graphs framework extendible and very flexible, as noted in the next section.
The points in the previous section on extendibility are also relevant to the issue of flexibility. In addition to those points, the Constraint Graphs design is flexible in its implementation of its intrinsic model. The model is very easy to modify because most of the component constraints, such as "acyclic isa arcs" and "strictly-nested contexts", are implemented as ad-hoc constraints, which are very easy to modify if the need arises. These constraints exist as part of the constraint library and are added to the base type objects (node, arc, isa arc, and context) during program initialization. This not only makes it trivially easy to remove or replace these constraints, but also makes it easy for other type objects to re-use the same constraints (without any programming).
Such challenges have played a major role in the development of the Constraint Graphs theory. For example, the theory was extended to include multiple ontologies when the implementation of KDraw showed the need for both a semantic and a visual ontology (as described in Section 4.3.6). The framework failed to allow the desired behaviour (individual's inheritance of attribute-value pairs from concepts while baring the application of concept's constraint behaviour). In this case, the failure indicated a deficiency in the theory, which lead to its extension to include multiple type lattices, which was implemented as ontology filters in the framework.
In addition to the languages described in Chapter 7, several other languages have been defined using the Constraint Graphs framework with varying degrees of success. One of these languages was a new language (which was originally designed using Constraint Graphs) called Annotated Flow Chart (Kremer, Lukose & Gaines 1997). This language is an extension to flow charts and presented no challenge at all for Constraint Graphs. In contrast, some of the object oriented notations were also implemented, and these presented some challenge to Constraint Graphs. The problem here involved contexts, which are probably underdeveloped in the present theory. In these implementations, methods where modeled as nodes that could only be contained inside classes or objects (which were modeled as contexts). While ad-hoc constraints could be used to solve the problem, it seems natural that there should be a way to model such constraints visually, just as arc termination constraints are visually specified in a natural way. Exactly how this could be done, or even if it should be done, is open to debate.
Contexts themselves present an issue in the theory. It is debatable whether or not contexts belong in a theory of concept maps. Many concept mapping languages lack the notion of context; for example, neither gIBIS nor KDraw contain any notion of contexts (although KDraw allows one to draw a context, it has no semantic meaning whatsoever). On the other hand, Conceptual Graphs embraces context as a fundamental notion. The current theory allows for the use of contexts, but contexts can be easily constrained away for languages that do not use context. The contexts in the theory follow Conceptual Graphs in that contexts are strictly nested and cannot be "overlapped" (Section 4.3.2.4). This is a contentious point since using this constraint does not admit such languages as Venn diagrams and Euler circles (Hammer 1995). However, elimination of these languages is probably justified in that it is easy to judge Venn diagrams and Euler circles as not being concept maps since their semantics (and lack of arcs) is substantially different from most "obvious" concept mapping languages.
There is much future work in implementation of both existing and new concept mapping languages in the framework. The expectation is that this will lead to a better and more complete theory of concept mapping languages.
One may also formulate a theory that is the extreme opposition to the node-centric theory. It is possible to eliminate nodes from the theory entirely and view nodes only as arcs with an arity of zero. This arcs-only theory has the appeal of greater simplicity and homogeneity, since it eliminates one of the four fundamental types (nodes) in the theory. It also allows for a straight- forward description of arcs whose type label is an entire subgraphs, since such an arc is merely a context with arity greater than zero. The main drawback of the arcs-only theory is that it may be viewed as too radical and therefore difficult for many researchers to accept. This theory is viewed by the author as important, and will be tested by a variant of the framework in the near future.
It is therefore very compelling to add the remaining Conceptual Graphs formation rules as Constraint Graphs manipulation operators. This would achieve a complete implementation of Conceptual Graphs within Constraint Graphs. The four Conceptual Graphs formation rules and their likely implementation under Constraint Graphs is as follows:
This section describes potential future work to be undertaken to extend Constraint Graphs beyond its present functionality.
A relatively simple translator has already been shown in Section 8.1. This translator converts a system developed in Constraint Graphs to a Z specification. While this may be useful for Z-literate users in understanding a system, the generated Z notation is considerably more verbose and hard-to-understand than the original Constraint Graphs definition. Although it is a useful demonstration, it is of limited utility.
More useful would be translators to other systems. For example, the KDraw Constraint Graphs system described in Section 7.3 could be translated into the KDraw version of CLASSIC, and passed to a KDraw engine where inferences could be made. If the translator could also translate back to native Constraint Graphs format, the inferences could be used as updates to the original graph, giving the user the impression that the graphical interface "knows" how to do inferences.

Figure 50 shows just such a situation. The Constraint Graphs process is using the KDraw definition described in Section 7.3, which describes KDraw syntax. The translator, built similarly to the Z translator, converts the user's definition into KDraw's CLASSIC-like representation language and sends the result to a KDraw process. The KDraw process is a server that may reside on the same machine, or may reside elsewhere on the Internet. A simple server protocol modeled on the HTTP protocol would suffice. The translator could also easily invoke the KDraw process (on the local machine) if it where not already running. This is not unlike the current KDraw "compilation" in the current version of KRS.
Platform portability is not a large issue for the main part of Constraint Graphs since it is written is ANSII C++ and avoids the use of platform specific features. On the other hand, the CMap interface portion of Constraint Graphs is highly machine dependent because it cannot avoid using graphical routines and system routines (such as menu manipulators) that are highly platform-dependent. Steps have been taken to isolate this platform dependence: all system-dependent calls have been abstracted to platform-independent generalizations, and are contained in a code library and accessed indirectly by the programs through this library. This allows one to accomplish most of the work of a porting the framework to another platform by simply replacing the platform-dependent library.
Nonetheless, porting the interface to another platform still entails considerable effort both in terms of the initial work and ongoing support. Most of this work could be avoided by rewriting the interface in a platform-independent language, as Java is currently shaping up to be. As discussed in Section 8.2.1, re-writing all of Constraint Graphs does not seem to be a viable option; but, fortunately, Java is well equipped to interface with other languages, thanks to its "native method" facility. Java native methods are methods that do not have a Java body, but call a function in a run-time library using a standard protocol: they act just like Java methods, and so present a very clean interface to methods written in other languages.
It would not be difficult to interface a Java version of CMap to the current version of Constraint Graphs, where the two system communicate through "native" Java methods. In support of this goal, Java versions of the CMap library and the CMapper program have been developed at the University of Calgary (Flores-Mendez 1997). Since the Java programs include both a stand-alone version and a Web-browser embedded version, these programs form a good basis for Java-integrated Constraint Graphs versions.
The Constraint Graphs groupware version described in Section 8.3 should not be viewed as anything more than a prototype. Much more work needs to be done to make Constraint Graphs a viable groupware application. Among the needed improvements are:
This thesis has described concept mapping languages as a sub-kind of visual languages. Even though concept maps are characterized by simple nodes and connecting arcs, the design space of concept mapping languages is large. This contention is supported by the large number of concept mapping languages in existence and the number of fields that concept mapping languages have been applied to. In order to design new concept mapping languages and to investigate variations on existing concept mapping languages, one must avoid the significant effort usually required to build graphical languages. This thesis addresses the problem by developing a general-purpose framework in which concept mapping languages can be quickly prototyped to a working application where the new (or modified) languages can be investigated.
The thesis has described visual languages, their value, semantic models, and classification. Concept mapping languages are distinguished from the more general visual languages by their distinct nodes and arcs. Several concept mapping languages are described in some detail. Since component type is an important concept in all formal concept mapping languages, the thesis describes type theory in the context of object oriented programming, graph grammars, and hypergraphs.
A detailed requirements analysis for the Constraint Graphs framework is developed in chapter 4. The formal specification (in Z) of Constraint Graphs is described in chapter 5, which amounts to a minimal theory of concept mapping languages. The design of the framework software is described in chapter 6. These chapters serve to describe the framework in detail.
Chapter 7 describes how the framework can be used by defining three different concept mapping languages: gIBIS, Conceptual Graphs, and KDraw. New languages can be defined by visually adding new nodes and arcs to the type lattice. These represent the component types of the defined language. Subtype/supertype relationships are visually defined by drawing isa arcs between the subtype component and its supertype component. These components will be used in type inference in the final language. A layering construct allows a language design to filter out generalization and other details that should no be available to the end user. More advanced language constructs can be defined using attribute/value pairs and ad-hoc constraints.
Chapter 8 describes extensions to Constraint Graphs, including translation of Constraint Graphs definitions into Z, a Netscape plug-in version of the framework, and the groupware version.
This final chapter has described how the research has met its original objective of creating a concept mapping framework by implementing several existing concept mapping languages. It also describes issues of efficiency, scalability, expressiveness, completeness, extendibility, and flexibility. Finally, some possible avenues of future work are described:
 Chapter 8
Chapter 8
 index
index
 References
References
 Constraint Graphs: A Concept Map Meta-Language (PhD Dissertation), Department of Computer Science
Constraint Graphs: A Concept Map Meta-Language (PhD Dissertation), Department of Computer Science