 Rob Kremer
Rob Kremer

 preamble
preamble
 index
index
 Chapter 2
Chapter 2
This chapter begins by briefly describing visual languages and a general kind of visual language: concept mapping languages. The many existing visual languages (and concept mapping languages in particular) are used in many different disciplines for widely diverse purposes. Computer support of concept mapping languages allows for easy editing and provides computational facilities such as those for the enforcement of syntactic and semantic constraints.
One of the problems with visual languages is the effort involved in creating a program to support each and every language. This thesis introduces Constraint Graphs, a computational environment to support the visual description of concept mapping languages that also uses the description to yield an implementation of the target language. Constraint Graphs also addresses the problem of lack of formal specification in visual languages. Several authors have addressed the specification issue, but have done so in a textual, predicate logic formalism. Visual languages should best be specified in visual languages. Constraint Graphs, by its own formal semantics and simple model, is a step toward a visual specification of concept mapping languages.
The last section of this chapter gives an overview of the software engineering aspects of the Constraint Graphs implementation.
Concept mapping is related to several distinct research areas, including knowledge representation (Sowa 1991), graph theory (West 1996), graph grammars (Cuny, Ehrig & Engels 1994), and hypertext (Conklin 1987). Each of these areas deals with graphs - nodes with arcs that interconnect the nodes. Each of these areas is relatively independent, and all tend to use different terms for very similar, if not identical, concepts. The term node in concept mapping is called a vertex in graph theory, and a concept in many sub-disciplines of knowledge engineering. The term arc is called an edge in graph theory, a relation in many sub-disciplines of knowledge representation, and a link in hypertext theory.
It is often difficult or confusing, when describing these other research areas, to use non-native terms. This thesis therefore uses the terms node, vertex, and concept interchangeably, and does the same with arc, edge, link, and relation. The preferred terms, however, will be node and arc.
The knowledge engineering community has developed a considerable number of formal knowledge representation languages including Ontolingua (Gruber 1995), CLASSIC (Borgida et al. 1989), Conceptual Graphs (Sowa 1984), and KIF (Genesereth & Fikes 1992). Some of these have graphical forms, such as KDraw (Gaines 1991b), which implements a completely visual version of CLASSIC. The graphical forms have considerable appeal because they present a relatively intuitive, two-dimensional view of the knowledge. In contrast, the purely textual languages tend to be useful only to experts who have invested considerable effort in understanding them.
define-concept[bird,(PRIMITIVE CLASSIC-THING Bird)].
define-concept[tubenose, (AND bird
(FILLS nostrils external-tubular)
(FILLS lives at-sea) (FILLS bill hooked))].
define-concept[fulmar, tubenose, fulmar].
define-concept[albatross,(AND tubenose
(FILLS size large)
(FILLS wings long-narrow))].
define-concept[layson-albatross albatross].
define-concept[black-footed-albatross, (AND albatross
(FILLS color dark))].
assert-rule[black-footed-albatross, (FILLS name Black-footed-Albatross)].
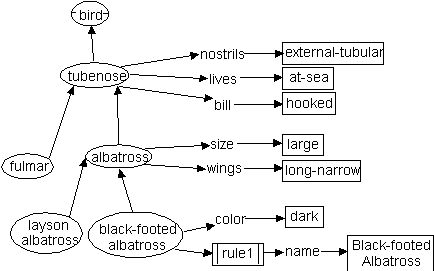
For example, Figure 1 shows part of a CLASSIC knowledge base on bird identification that describes a section of the class-to-species hierarchy immediately above black-footed albatross. It describes several observable attributes that can be used to identify an observed bird successively as a tubenose (by having external, tubular nostrils; a hooked bill; and living at sea), as an albatross (by being large and having long, narrow wings), and finally as a black-footed albatross (by having dark coloration). To a non-specialist, Figure 1 seems rather opaque. On the other hand, Figure 2 (described in Section 2.3.1), which is the visual version of the same portion of the same knowledge base, is more readily understood (Nosek & Roth 1990). Even a casual observer could guess that the graphical version is composed of a classification hierarchy on the left side and attributes of the of the classes on the right side. The detailed meaning of the classification may not be obvious to the casual observer; but to people knowledgeable in CLASSIC, the two dimensional layout makes all the relationships immediately and abundantly clear. Although the same information is conveyed by the textual version, the reader must exert considerably more cognitive effort to match up all the identifiers in order to mentally construct the hierarchy and relationships that are obvious in the graphical version.
There is still little hard evidence to support the value of graphical languages, or visual languages as they are now popularly referred to. But Nosek and Roth have undertaken empirical studies that indicate that (visual) semantic networks are more understandable than (textual) predicate logic (Nosek & Roth 1990). There are also large numbers of graphical, or visual, languages for a wide variety of purposes, including programming, program visualization, design of various kinds, decision making, network control, database query, and natural language generation and comprehension. Smith makes many arguments about the psychological motivations for using visual languages (Smith 1977) (see Section 2.1.1).
Visual languages are useful for many purposes other than knowledge representation. Several authors (Myers 1990; Price, Baecker & Small 1993) have developed taxonomies for the ever-increasing variety of visual languages. These taxonomies range not only over the purpose of the visual languages, but also over their specification technique. This thesis focuses on knowledge representation - though it does diverge occasionally into other intended purposes. But this leaves still too wide a range of languages. So the focus is narrowed to a (still very broad) subset of visual languages, called concept maps.
The term concept map is a general term describing a type of visual language. Concept maps consist of labeled nodes with (possibly labeled) arcs connecting the nodes. They are akin to graphs in mathematics.
There are a large number of concept mapping languages: of Myers' (1990) 14 taxonomy categories of visual languages, 6 categories are concept mapping languages. Furthermore, 24 of the 39 visual languages Myers studied were concept map languages. Concept maps have been used in many areas, including education (Lambiotte et al. 1984; Novak & Gowin 1984), management (Axelrod 1976; Hart 1977; Eden, Jones & Sims 1979; Banathy 1991), artificial intelligence (Quillian 1968), knowledge acquisition (McNeese et al. 1990), linguistics (Sowa 1984; Graesser & Clark 1985), programming (Burnett & Baker 1994), program design (Cox 1991; Booch 1994; Coad, North & Mayfield 1995), and program visualization (Myers 1990).
Concept maps are not just unconstrained graphs. Concept maps extend over a wide range of formality. Concept maps may be very informal and free form, such as "webs" used in education to allow students to describe their conceptual knowledge to teachers (see Figure 3, which shows a concept map developed by an unsupervised six-year-old boy using a concept mapping software package). Informal concept maps are very easy for people to create, because of the lack of constraints. They are therefore useful in education, in brainstorming, in the early stages of knowledge acquisition, and in any situation where the effort of conforming to a formalism may be too costly or time consuming, such as note-taking during a business meeting.
Concept maps may also be very formal and constrained. Figure 2 is an example of a formal concept map. Formal concept maps are not as easy for humans to create and usually require some degree of expertise, but their formality allows them to be interpreted by computers, which enables various forms of computational support. For example, formal concept maps are used to create expert systems (Gaines 1991b) and as complete programming languages (Smith 1977; Lukose 1993).
The formality of concept maps is not a discrete classification, but a continuum from informal to formal, with many shades of semi-formal languages in between. Semi-formal concept mapping languages strike a balance between human comprehension and the possibility of computational support. Examples of semi-formal concept mapping languages are gIBIS (Conklin & Begeman 1987), used in decision making, and object-oriented program design languages such as Booch notation (Booch 1994) and OMT notation (Coad, North & Mayfield 1995).
Concept maps are difficult to draw using pen and paper because the two dimensional layout requires the author to predict the two dimensional extents in advance of starting to draw. Furthermore, additions and modifications to a graph often entail moving or rearranging large subsets of the map, which would mean much erasing and recopying if done with pen and paper. Computerized concept mapping tools help, not only by facilitating easy copy and move operations, but by enabling a broad range of constraints on layout, syntax, and semantics, depending on the language.
The previous section mentioned many different domains in which concept maps are used, and in most of these domains many different concept mapping languages are used. For example, software engineering alone uses object model notation, Booch notation, entity relation diagrams, data flow diagrams, Rumbaugh notation, structure charts, Petri nets, and others. It is clear that there are a vast number of concept mapping languages (and more to come in the future). If all of these are to be provided with computer support, it is clear that it can not be in the form of individual, specialized programs for each concept mapping language. The required software development effort is just too great. Many possible languages would not have computer support, and those that do would not be easy to modify in order to "evolve" the notation. Some way to ease the design of, development of, and experimentation with concept mapping languages must be found if concept mapping languages are to fulfill their potential as an expression medium.
Myers (1990), in his oft-cited (and three times published) taxonomy of visual languages, points out several problems with visual languages. Among those problems are:
These problems will be addressed in this thesis.
It is not easy to create a visual concept mapping language tool. The complex graphics, direct manipulation user interaction model, object tracking, and constraint maintenance add up to a very complex system that is difficult and time consuming to specify, design, and build. The effort is not worth it for every potential visual language.
A framework for the fast development and modification of concept mapping languages would be very useful. Among the potential benefits are:
This thesis describes such a framework tool, called Constraint Graphs. Constraint Graphs provides an environment in which a large variety of concept mapping languages can be described using a simple concept mapping language. The new language description allows Constraint Graphs to behave like a program custom-made for that language, enforcing its syntactic (and some of its semantic) constraints.
Constraint Graphs is a distillation of many of the common features found in concept mapping languages. It is centered around a simple type theory. There are nodes and arcs which are mutually exclusive of one another. There may be any number of user-defined subtypes of nodes and arcs. The end points (or terminals) of arcs may be anchored on nodes or other arcs (arcs between other arcs are rarely, but sometimes, used in concept mapping languages). To describe an object type, the user merely draws it on the screen. To make one object a subtype of another, the user just draws a special type of arc (an isa arc) from the subtype to the supertype object. The types of the objects at each of an arc's terminals constrain all its subtype arcs to terminate on only subtypes of the corresponding objects.
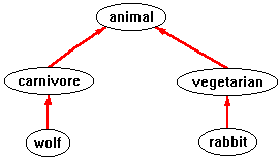
For example, one can define a domain of carnivores and vegetarians, where both are classified as subtypes of animal:
Here, the unlabeled, red arcs are isa arcs, representing the subtype relationship. In order to describe the fact that carnivores eat other animals, one creates an eat relationship between carnivore and animal by drawing in a new arc (labeled eat) between the carnivore node and the animal node:
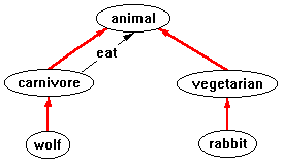
Given this simple definition it is legal to draw an eat arc between wolf and rabbit:
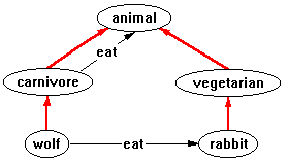
because wolf is a subtype of carnivore and rabbit is a subtype of animal. If the user attempted to draw the arc in the reverse direction (from rabbit to wolf), the system would disallow it because rabbit is not a subtype of carnivore, and there is no other eat relationship that is legal.
In addition to just evaluating the legality of arcs, the system is capable of making type inferences: in the example above, the user need only indicate an arc from wolf to rabbit; the system can automatically type the relationship as eat because that is the only legal relationship between those two node types in the domain. Constraint Graphs can also associate attributes, such as surround shapes, colors, line types, and arbitrary user-defined attributes with objects, and can propagate these attributes and their values through the type (isa) hierarchy.
Using such simple techniques, Constraint Graphs can model many different concept mapping languages to provide a specialized interface for the target language. This ability to quickly prototype and implement visual languages shortcuts the expense of custom development efforts to allow the design and implementation of - and experimentation with - many new visual languages.
Chapter 6 describes many of the techniques used in Constraint Graphs for describing visual languages, and chapter 7 presents case studies of Constraint Graphs specification of several popular concept mapping languages (two knowledge representation languages and a semi-formal decision making language).
Myers' wish for formal specification of visual languages is addressed by Constraint Graphs. Constraint Graphs itself is formally specified in the Z formal specification language (Hayes 1987; Spivey 1989). Chapter 5 describes Constraint Graphs' formal specification. Constraint Graphs' formal semantics, together with its very simple model, means that any language implemented on top of Constraint Graphs is well specified. A section in chapter 8 describes Constraint Graphs' ability to generate a Z specification of any language implemented in it.
While Constraint Graph's formal specification does not necessarily constitute a useful formal specification for Constraint Graphs-implemented languages, it does support the work of Crimi, Guercio, Nota, Pacini, Tortora, and Tuccit (1991) and Wang and Lee (1993) in visual language formal specification. Crimi et al describe a relational grammar formalism which serves to specify the syntax of a visual language. Wang and Lee describe a formal semantics for an interpretation that maps a visual language onto a domain language. Constraint Graphs' structure is consistent with both of these works, so avails itself to these formal descriptions as well.
Both the work of Crimi et al and Wang and Lee are textual predicate calculus descriptions of visual languages. However, it is intrinsically appealing to specify visual languages in a visual language. Constraint Graphs, by its very nature, does just that: concept mapping languages are described in terms of concept maps which have a formal definition.
Adopting a principled approach to system design and implementation is particularly important for a project like Constraint Graphs because it is more than just a program: it is a developing and evolving theory. For example, the first iterations of system design involved only node, binary arc, and isa objects as primitives; but as the design progressed it became obvious that the notions of n-ary (non-binary) arcs and contexts (graph partitions) needed to be included in the system, and that they could be included in a consistent manner. It seems inevitable that the need for other new facilities will arise as more and more concept map languages are implemented on top of Constraint Graphs.
The Constraint Graphs program is an object oriented program written in C++. It has been carefully designed to be very modular. It has a very distinct separation between large scale modules with a very defined interface between them: the Constraint Graphs "engine" (that implements the graph database and enforces constraints) is entirely separate from the user interface that actually draws the concept maps. The interface has been used without Constraint Graphs as a stand-alone, unconstrained, concept map drawing program. When Constraint Graphs and its interface are used together, the two components may be configured to run on different machines - due to the command-oriented interface between the two.
Constraint Graphs is designed for maximum flexibility. It is designed to run under a windowing operating system, but the details of the operating system have been abstracted away into a minimal windows library to enhance its portability. Furthermore, the interface is largely implemented within a "graphics" library, which allows a Constraint Graphs program to be configured as a stand-alone program; as a multi-user, real-time interaction program; or as a plug-in component to World Wide Web browsers, such as Netscape (again, either single- or multi-user).
At a finer level of granularity, the classes have been designed to faithfully conform to a type lattice, and the recently emergent programming patterns paradigm (Gamma et al. 1995; Pree 1995; Buschmann et al. 1996) has been adopted to increase the comprehensibility of the program by other programmers. Wherever possible, functionality (including those of the patterns) has been abstracted into independent classes and the "mix-in" (multiple inheritance) paradigm has been used to combine functionality.
Templates (type-parameterized classes) have been heavily used to abstract commonality between similar (but type-distinct) classes. For example the command objects of the command pattern (Gamma et al. 1995) have been implemented as a set of templates that can carry any object type in a type safe manner. The ANSII standard C++ STL (Standard Template Library) (Nelson 1995; Stepanov & Lee 1995) has also been extensively used for type safe container classes.
The primary objective of this thesis is to provide the basis for a concrete theory of concept mapping language syntax by developing a software framework for the development and implementation of concept mapping languages. The work will narrow its focus somewhat to concentrate on knowledge representation languages.
The theory is a minimal, empirical theory. It is an empirical theory in that it attempts to describe a significant sub-class of visual languages known as concept mapping languages. It is minimal in the sense that it attempts to describe a very broad range of concept mapping languages without eliminating any languages unnecessarily – an attempt is made to avoid "over-specializing" the description while still capturing all of the essentials of concept mapping languages. It should be noted that the theory is meant to be criticized; it should be extended to encompass more (and new) concept mapping languages, and simplified to be as simple and as clear as possible. It is only one of many possible theories of concept mapping languages ( Chapter 9 alludes to several other possible theories).
The framework acts as a concrete model of the theory, and should be flexible enough to encompass the fundamental syntax (and some semantics) of a wide selection of knowledge representation languages. The theory and framework will be tested by implementing language-specific environments for several existing knowledge representation languages. The framework-implemented language-specific environments should automatically enforce syntactic (and some semantic) constraints in a manner similar to the way a custom-coded environment would.
Since the concept mapping framework is intended to be a model of a developing theory, it is critically important that the framework be clearly described and cleanly constructed. This leads to two auxiliary objectives:
To provide a formal, rigorous, and unambiguous description, parts of the framework will be formally specified in the Z specification language. Note that not all of the framework should follow such rigor: the actual concept map drawing tools are not (and should not be) a part of a theory of concept maps, so the effort of rigorous specification is unwarranted.
It does no good to have a rigorous specification if the program developed from the specification is not a reliable implementation of the specification. It is therefore considered important to develop the framework in a principled manner, taking advantage of current technology such as design patterns (Gamma et al. 1995; Pree 1995) and the C++ Standard Template Library (STL) (Nelson 1995; Stepanov & Lee 1995). Furthermore, a straightforward correspondence between specification and implementation is also considered important, which entails favoring implementation decisions which enhance the direct correspondence to the specification over efficiency and similar considerations.
Further details about these objectives may be found in Section 4.1.
This chapter has briefly introduced visual languages and concept maps, especially with respect to visual knowledge representation languages. Concept mapping languages comprise a broad subset of visual languages, and are useful in many different disciplines for many different purposes. Concept maps range from the informal (free-form for ease-of-use) to the very formal (very constrained for computer support). Computer support for concept mapping is a real need to allow for easy editing and for explicit enforcement of syntactic and semantic constraints.
However, one of the problems with visual languages is the difficulty of writing programs to support them. Constraint Graphs addresses this problem by providing a visual (concept mapping) environment in which new concept mapping languages can be described. Constraint Graphs can then use such a description to "implement" the new language.
Another problem with visual languages is the lack of formal specification. This problem has been addressed by several authors but by using a textual predicate logic. Constraint graphs addresses the specification issue by providing a simple "platform" theory that is visually expressed in terms of concept maps. Visual languages are probably best specified in visual languages. Constraint Graphs is a start in this direction.
Since the Constraint Graphs program is seen as supporting an evolving theory, it is critical that it be designed to be as flexible and easy-to-understand as possible. The object-oriented software development paradigm, formal specification, and the recently emergent programming pattern paradigm have been adopted to provide this flexibility in design and implementation.
The primary objective of this thesis is to develop a software framework for the development and implementation of a variety of concept mapping languages. The framework should be able to serve as a test bed for a developing theory of concept mapping languages. To accomplish this goal, the framework must be rigorously specified where appropriate and implemented in a principled manner.
Chapter 2 describes visual languages and concept maps in detail and examines concept mapping's relationship to several other areas of study such as relational grammars and graph grammars.
Chapter 3 deals with types and the object oriented programming paradigm, then shows how these are related to concept maps. Concept maps as hypergraphs are discussed and current work on flat-typed hypergraphs is slightly extended to explain hypergraphs with types arranged in a type lattice. There is a short section at the end of Chapter 3 on formal specification by way of an introduction for the specification later in the thesis.
Chapter 4 describes the requirements analysis for the Constraint Graphs project. Most of this work deals with the abstract implementation of the Constraint Graphs database, which is responsible for the graph operations and constraint maintenance. The interface requirements are also described, but only briefly.
Chapter 5 deals with the formal Z specification of a Constraint Graphs system. Only the abstract database and graph operators are specified: the interface specification is much less formal since it is seen as just a replaceable component.
Chapter 6 describes the actual implementation based on the specification. It describes the separation of the main modules, the interface and actual Constraint Graph class libraries, the intended usage scenarios, and several important technical details.
Chapter 7 describes three concept mapping languages, and how they are implemented on top of Constraint Graphs. The implementation of gIBIS, a very simple decision making language, is described in detail. This serves to guide the reader through a very simple implementation to gain a flavor of Constraint Graphs definitions. Subsequently, the more complex and harder-to-implement knowledge representation languages, Conceptual Graphs and KDraw are described, building on the previous language descriptions.
Chapter 8 describes Constraint Graph's Z translator (which can translate a concept map definition into a Z specification); the World Wide Web browser-embedded version of Constraint Graphs; and a multi-user version of Constraint Graphs.
Chapter 9 is an evaluative conclusion and includes directions
for future work.
 preamble
preamble
 index
index
 Chapter 2
Chapter 2
 Constraint Graphs: A Concept Map Meta-Language (PhD Dissertation), Department of Computer Science
Constraint Graphs: A Concept Map Meta-Language (PhD Dissertation), Department of Computer Science