 Rob Kremer
Rob Kremer

 Chapter 4
Chapter 4
 index
index
 Chapter 6
Chapter 6
This chapter describes the specification of the Constraint Graphs system based on the requirements listed in the previous chapter. The design is split very firmly between the semantic engine (or abstract constraint graph), which is the heart of Constraint Graphs, and the user interface as per Requirement 1 (see Figure 16). It is only the semantic engine (the Constraint Graph itself) that is specified here. There is no formal specification for the user interface, although it is described in the following chapter.
The Constraint Graphs system is specified in a dialect of the specification language Z (Hayes 1987; Spivey 1989) called ZSL (Jia 1995). Z was chosen primarily because it is simple (based on set theory) and popular. Since the implementation paradigm is object-oriented programming (the system is implemented in C++), one of the object-oriented enhancements of Z (Stepney, Barden & Cooper 1992a; 1992b) would have been more appropriate. For example, inheritance polymorphism is extremely awkward to express in plain Z. Unfortunately, a good type checker for object oriented Z notations was not available at reasonable cost at the time of specification.
ZTC (Jia 1995) is a type checker for Z that is available in the public domain. It can take several syntactic dialects of Z as input: two Latex versions, and a pure ASCII text version. The pure text version is particularly appealing as it can be easily incorporated in standard HTML documents. Due to a serendipitous coincidence of compatible syntax, ZTC will even type check an HTML document with embedded ZSL.
The following description of the specification is in bottom-up order. This is necessary for a type checker, since terms need to be defined before they are used. Unfortunately, this is rather awkward for people. Nonetheless, the description will follow the bottom-up order necessitated by the Z type checker. To mitigate this problem, an overview (Section 5.1) is provided to introduce the specification.
A more serious problem is that of modeling inheritance in Z. When modeling the supertype/subtype relationship, the definition of the supertype is usually given first. This can be done in Z by including the supertype schema in the subtype's schema definition. But since Z is not object oriented, it does not embrace inheritance. Thus, if there is a schema A, the definitions
---B-- ---C-- | A | A ------ ------
do not imply B<A (B is a subtype of A) or C<A. Furthermore, values of type B and C cannot be referred to using the common type. To get around this problem, inheritance is modeled in an "upside-down" way using free type definition. In the example above, A0, B0 and C0 are defined first as stand-ins for A, B, and C; these contain the definitions one would expect in A, B and C. Then a free type definition is used to capture a common reference for B0 and C0:
A_types ::= b << B0 >> | c << C0 >>
A can now be defined using A0 and a new attribute called Role which can reference objects of type B0 and C0:
---A------- | A0; | Role: A_types |----- | A0 -----------
Finally, B and C can be defined as just A's with a restriction over the Role attribute:
B =^= [A | Role in ran b] C =^= [A | Role in ran c]
Although this technique is awkward and rather opaque, it does capture the typing that inheritance would yield (B and C are just specialized A's), and it passes the Z type checker just as though it where a true inheritance situation.
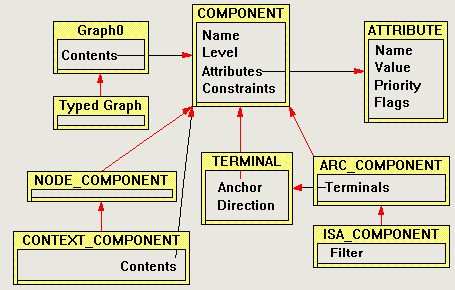
Figure 14 is an idealized diagram of the Constraint Graphs specification presented in this chapter. It is idealized because it shows an inheritance structure that is not possible to model directly in the Z specification language. Nonetheless, Figure 14 is very useful to explain the structure of the specification.
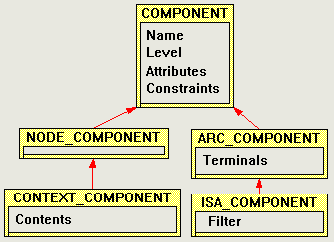
The five component "schemata" form a lattice almost identical to that of specified by Requirement 4 and diagrammed in Figure 11 (the only thing missing is the specific disjoint between the node and the arc types).
COMPONENT is specified as having a Name, a Level (Requirement 23), Attributes (Requirement 19) and Constraints (Requirement 15). Names support human usability and aren't really used for anything in the specification or the implementation, except to make things easier for the user to understand. Levels divide the components of graphs into categories. In general, lower-numbered levels contain the "primitive" components while successively higher-numbered levels contain progressively higher-order components. Levels are useful for several purposes, such as:
NODE_COMPONENT specializes COMPONENT, but does not particularly extend it. NODE_COMPONENT is nonetheless essential because COMPONENT is a "virtual" type which is never directly subclassed (except type NODE_COMPONENT and ARC_COMPONENT). The rule that NODE_COMPONENT and ARC_COMPONENT are mutually exclusive could not be enforced without NODE_COMPONENT. CONTEXT is a simple extension to NODE_COMPONENT which contains a subgraph of nested components. In fact, Figure 14 itself is drawn using Constraint Graphs, and the labeled boxes are CONTEXT_COMPONENTS that contain subgraphs: in this case, just simple NODE_COMPONENTS (with no shape surround).
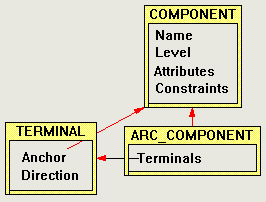
ARC_COMPONENT specializes COMPONENT and extends it with a sequence of Terminals which can, together, be physically represented by n-ary connection lines between components. All the arcs in Figure 14 are binary arcs, but higher-order arcs could be represented by forked lines of various sorts. ISA_COMPONENT specializes ARC_COMPONENT by adding an ontology filter in support of Requirement 18. ISA_COMPONENT also adds further constraints on isa arcs, such as "isa arcs are binary", which don't show up in the diagram but do show up in the specification.
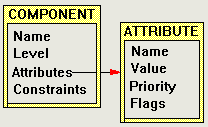
Components have sets of attributes as per Requirement 19 which consist of an attribute name, an arbitrary value of any type (but there are constraints to do with inheritance, Requirement 21), a priority to disambiguate in multiple inheritance situations, and some flags used to support Requirement 22 (preventing overriding of attribute values).
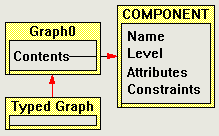
Graph0 is the basis of Constraint Graphs, and primarily acts as a container for the components. It also has responsibility to maintain a number of invariants among the contained components. TypedGraph is a specialization of Graph0 which adds to Graph0 the ability to enforce constraints in the components. Graph0 could not do this itself because constraints cannot be fully defined before Graph0 is defined.
Figure 15 shows a much more accurate depiction of the specification than does Figure 14. Since Z does not handle inheritance, it must be imitated in a rather opaque manner as described in the introduction to this chapter. Figure 15 shows the Z nesting (or inclusion) of specifications. The important inheritance relationship between COMPONENT, NODE_COMPONENT and ARC_COMPONENT has been turned into a COMPONENT with a free type definition, called "Role", which is defined as one (of any) of the subtypes in the Figure 14 model.
This section has provided an overview of the structure of the Constraint Graphs specification. The remainder of the chapter is devoted to the specification proper.
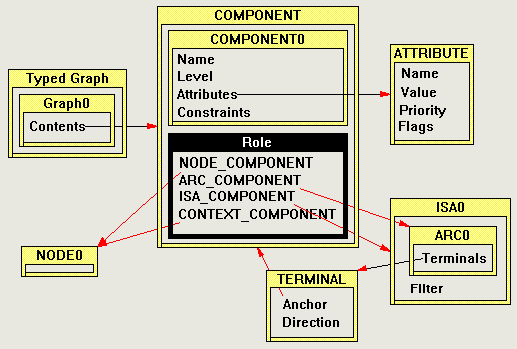
ATTRIBUTEs are used to tag graph components with application-specific attributes (Requirement 19). For example, the attribute "Shape" (Name) might describe the surround of a graph node with values (Value) such as "rectangle" or "ellipse". Attributes are meant to be inherited through the type system. The Priority field is used to arbitrate in the case of conflicts arising from multiple inheritance of an attribute. The Flags field is used to tag attributes with special properties such as CONSTANT, which prevents subtypes from overriding the value of the attribute (Requirement 22), and PRIVATE, which prevents subtypes from being able to "see" the attribute.
[char, ATTRIBUTE_NAME] ATTRIBUTE_VALUE ::= pos_int << N >> | int << Z >> | string << seq char >> | attribute_value: ATTRIBUTE_VALUE % generic value ATTR_FLAGS ::= CONSTANT | PRIVATE ---ATTRIBUTE------------------------------------------------------------- | Name: ATTRIBUTE_NAME; | Value: ATTRIBUTE_VALUE; | Priority: Z; | Flags: P ATTR_FLAGS; -------------------------------------------------------------------------
The ATTRIBUTE_VALUE specification above is not intended to be an inclusive set of type possibilities: The implementation would be expected to extend the types as necessary.
MakeAttribute is a convenient function to create a new attribute.
| MakeAttribute: ATTRIBUTE_NAME & ATTRIBUTE_VALUE & Z & P ATTR_FLAGS | --> ATTRIBUTE |----------- | MakeAttribute = | (lambda n:ATTRIBUTE_NAME; v:ATTRIBUTE_VALUE; p:Z; f:P ATTR_FLAGS @ | (mu a:ATTRIBUTE | a.Name=n /\ | a.Value=v /\ | a.Priority=p /\ | a.Flags=f))
Ontology filters support the ability to overlay multiple ontologies within a single graph (Requirement 18). Recall from Requirement 9 that type lattices (or ontologies) are formed by isa arcs between the graph's components. By tagging isa arcs with information as to whether it applies to a particular ontology, one can examine any particular ontology by merely ignoring all the isa arcs that are not applicable. This is done with ontology filters.
To begin with, assume that each ontology has a unique identifier:
[ONTOLOGY_ID]
An ontology filter is then just a set of ontology identifiers:
| OFilter: P (P ONTOLOGY_ID);
Thus, when one is examining a type lattice, one need only check to see if each of the defining isa arc's ontology filters contains the ontology identifier of the ontology (or ontologies) of interest. Note that there is no reason to focus on any particular ontology identifier, but rather a set of ontology identifiers may be compared against a filter.
The above description is a bit over-simplified. Quite often, one wants to check a component's ancestry over any ontology, so one uses the set of all ontologies (the universal ontology) as the ontology of interest.
UniversalOntology == ONTOLOGY_ID
This is simple enough, but it is possible that, even when using the universal ontology, there may be a chain of isa arcs that cannot be followed. For example, in the following diagram,

the isa arcs are labeled with the set of ontology identifiers, and X and Y are distinct ontology identifiers. Naively, one might assume that C<A (C is a subtype of A), but this is not so. Since X and Y are distinct, C is not related to A at all. Even when one starts out from C with the universal ontology as the ontology set, the ontology set should be restricted by the filter on the CB isa arc,
ontology filter(CB) = UniversalOntology {Y} = {Y}
which causes the BA isa arc to be ignored:
{Y} filter(BA) = {Y} {X} =
The following relation captures this concept:
%% inrel accepts
| _ accepts _ : OFilter <-> OFilter
|-----------------------
| forall f,f2:OFilter @
| (f accepts f2) <=> ((f && f2) /= {})
Both the set of interest ontologies and the filter are considered ontology filters.
COMPONENT0 is the common part of both the graph nodes and the arcs among the nodes. All components have:
[VALIDATOR, NAME] ---COMPONENT0------------------------------------------------------------ | Name: NAME; | Level: Z; | Attributes: P ATTRIBUTE; | Constraints: P VALIDATOR; -------------------------------------------------------------------------
COMPONENT is a specialization of COMPONENT0 that is meant to be the supertype of nodes, arcs, isa-arcs, and contexts (Requirement 4), but one needs to first define arcs, isa-arcs and contexts (since they all refer to COMPONENTs). Therefore COMPONENT is pre-declared here.
[COMPONENT]
CONTENTS is the contents of a node, which will be left up to the application and so is just defined generically. But CONTEXT will be a sub-type of node, and its contents will be a set of other components; so this is explicitly mentioned as a possible CONTENTS type.
CONTENTS ::= GENERIC_CONTENTS | members << P COMPONENT >>
NODE0 is the node-specific extension to COMPONENT0. It has some unspecified contents.
---NODE0----------------------------------------------------------------- | Contents: CONTENTS; -------------------------------------------------------------------------
Arcs take a little more work to specify than nodes. Arcs are very general in this specification: they have an arbitrary arity (they need not be binary, Requirement 5), are ordered (Requirement 6), and they may terminate at an arbitrary component (either nodes or other arcs, Requirement 7). The terminals of an arc have direction besides a reference to the anchor component. All arcs must have at least one terminal (Requirement 5).
DIRECTION ::= FROM | TO | BIDIRECT | NONE ---TERMINAL-------------------------------------------------------------- | Anchor: COMPONENT; | Direction: DIRECTION; -------------------------------------------------------------------------
ARC0 is the extension of COMPONENT0 for arcs.
---ARC0------------------------------------------------------------------ | Terminals: seq TERMINAL; |--------------- | #Terminals > 0 -------------------------------------------------------------------------
Isa arcs are a subtype of arc with an ontology filter (Requirement 18) and a restriction that they be binary (Requirement 8).
---ISA0----------------------------------------------------------------- | ARC0; | Filter: OFilter; |--------------- | #Terminals = 2 ------------------------------------------------------------------------
Finally, the parts can be brought together to define a component. The basic components of a graph are nodes, arcs, and isa arcs. A COMPONENT is the base, COMPONENT0 (name, level, and attributes) together with the NODE0, ARC0, or ISA0 extension.
COMPONENT_TYPES ::= node << NODE0 >> | arc << ARC0 >> | isa_arc << ISA0 >> ---COMPONENT------------------------------------------------------------- | COMPONENT0; | Role:COMPONENT_TYPES; |------------- | COMPONENT0; -------------------------------------------------------------------------
NODE_COMPONENT, ARC_COMPONENT, ISA_COMPONENT, and CONTEXT_COMPONENT are simply conveniences to refer to arcs, nodes, isa arcs, and contexts. Contexts are just nodes that contain other graph components (Requirement 10 and Requirement 11).
NODE_COMPONENT =^= [COMPONENT | Role in ran node] ARC_COMPONENT =^= [COMPONENT | Role in ran arc] ISA_COMPONENT =^= [COMPONENT | Role in ran isa_arc] CONTEXT_COMPONENT =^= [COMPONENT | Role in ran node /\ (node~Role).Contents in ran members]
NULLCOMPONENT is a special value used to represent "dangling" arcs (Requirement 17).
| NULLCOMPONENT: COMPONENT
MakeTerminal is a convenience function to create a terminal:
| MakeTerminal: COMPONENT & DIRECTION --> TERMINAL |--------------- | MakeTerminal = (lambda c:COMPONENT; d:DIRECTION @ | (mu t:TERMINAL | t.Anchor=c /\ t.Direction=d))
The functions Terminal and TerminalDir are conveniences to extract individual terminals and direction of individual terminals from arcs.
| GetTerminal: ARC_COMPONENT & N +-> COMPONENT; | GetTerminalDir: ARC_COMPONENT & N +-> DIRECTION; |-------------- | forall a:ARC_COMPONENT; n:N | n <= #(arc~(a.Role)).Terminals @ | GetTerminal(a,n) = (((arc~(a.Role)).Terminals)(n)).Anchor /\ | GetTerminalDir(a,n) = (((arc~(a.Role)).Terminals)(n)).Direction;
The GetFilter function is a convenience to extract the filter from an ISA_COMPONENT .
| GetFilter: ISA_COMPONENT --> OFilter; |-------------- | forall a:ISA_COMPONENT @ | GetFilter(a) = (isa_arc~(a.Role)).Filter;
The incontext relation is a convenience to determine whether or not a particular component is a member of a context.
%% inrel incontext | _ incontext _ : COMPONENT <-> CONTEXT_COMPONENT |-------------- | forall c:COMPONENT; x:CONTEXT_COMPONENT @ | c incontext x <=> c in members~((node~(x.Role)).Contents)
So far, the discussion has centered around the parts of a simple graph; however, the intent is to describe typed graphs. Nodes and arcs all have one or more supertypes. In this specification, types are just other components of the graph (Requirement 2 and Requirement 3). A type or object is a subtype or instance, respectively, of another by virtue of being connected to it by a special arc type called ISA_COMPONENT (Requirement 9).
The parts of a graph (nodes, arcs, isa arcs, and contexts) are themselves type objects in this theory. A node is called "Node", etc.
| Node,Arc,IsA,Context,T: NAME
The four components (plus the defining isa subtypes between them) all reside uniquely in the highest type level (level 1). A graph always contains the basic components: node, arc, context, and isa.
Within a graph, one can describe the traditional subtyping relations. Here the relation parentof refers to only immediate parents, while the relation ancestorof is the normal proper supertype/subtype relation. Isa is as expected: just the same as ancestorof except that identity is included. Note that the direction of the isa relation is the reverse of the other two!
%% inrel parentof %% inrel ancestorof %% inrel isa
There are several constraints on a GRAPH0:
In order to more conveniently talk about isa chains, it is necessary to define a path. A PATH is a sequence of COMPONENT pairs (together with the relevant filters) that leads from any COMPONENT to an ancestor.
PATH == seq ((COMPONENT & OFilter) & COMPONENT)
PATH is used in the definition of the function, paths_btwn, which will be used to examine ancestry relationships between components.
Finally, the definition of GRAPH0 follows. Note that this definition is incomplete because it does not include anything about constraints (which are called for by Requirement 15). This is because the definition of constraints (next section) requires the definition of a graph. The definition of a graph can be extended from GRAPH0 after constraints are defined in terms of GRAPH0.
---GRAPH0---------------------------------------------------------------
| Contents: P COMPONENT;
| TOP: COMPONENT;
| NODE: NODE_COMPONENT;
| ARC: ARC_COMPONENT;
| ISA: ISA_COMPONENT;
| CONTEXT: CONTEXT_COMPONENT;
|
| Level1Objects: P COMPONENT;
|
| _ parentof _ : COMPONENT & OFilter <-> COMPONENT;
| _ ancestorof _ : COMPONENT & OFilter <-> COMPONENT;
| _ isa _ : COMPONENT & OFilter <-> COMPONENT;
|
| % these next 3 awkwardly shadow the above due to syntax constraints
| parentof0 : COMPONENT & OFilter <-> COMPONENT;
| ancestorof0 : COMPONENT & OFilter <-> COMPONENT;
| isa0 : COMPONENT & OFilter <-> COMPONENT;
|
| paths_btwn : COMPONENT & COMPONENT & OFilter --> P PATH;
| get: N1 >+> Contents;
| getID: Contents --> N1;
|--------------
| getID = get~;
|
| {TOP, NODE, ARC, ISA, CONTEXT} = Level1Objects;
| forall c,p:Contents; o:OFilter @ (p->o)->c in parentof0 <=>
| (p->o) parentof c;
| forall c,p:Contents; o:OFilter @ (p->o)->c in ancestorof0 <=>
| (p->o) ancestorof c;
| forall c,p:Contents; o:OFilter @ (c->o)->p in isa0 <=>
| (c->o) isa p;
| Level1Objects subseteq Contents;
|
| % _ parentof _ : a little complicated because we need a special case
| % for ISA_COMPONENTs to prevent endless recursion of isa's
| %
| (forall p,c:Contents; o:OFilter | p /= ISA @
| (p->o) parentof c <=>
| (exists a:ISA_COMPONENT |
| a in Contents /\ GetFilter(a) accepts o @
| GetTerminal(a,2) = p /\ GetTerminal(a,1) = c))
| /\
| (forall p,c:Contents; o:OFilter | p = ISA @
| (p->o) parentof c <=> (c.Role in ran isa_arc /\ p /= c /\
| not (exists a:ISA_COMPONENT |
| a in Contents /\ GetFilter(a) accepts o @
| GetTerminal(a,2) = p /\ GetTerminal(a,1) = c)));
|
| % paths_btwn() : enumerates all the paths between a child and an ancestor
| forall c,p:Contents; o:OFilter @ paths_btwn(c,p,o) = {s:PATH |
| first(first(s(1))) = c /\
| (forall i:1..#s @
| s(i) in ( _ parentof _ ) /\
| second(s(i)) = (if i=#s then p else first(first(s(i+1)))) /\
| second(first(s(i))) = (if i=1 then o else
| Intersection {x:OFilter | (exists j:1..i-1 @
| x = second(first(s(j))))}))};
|
| % _ ancestorof _ : recursively accents the _parentof_ relation while
| % accumulating a more restrictive filter
| %
| forall c,p:Contents; o:OFilter @
| (p->o) ancestorof c <=> paths_btwn(c,p,o) /= {};
|
| % _ isa _ : simply the disjunct of the _ancestorof_ and
| % identity relationships
| %
| forall p,c:Contents; o:OFilter @ (c->o) isa p <=>
| ((p = c) \/ ((p->o) ancestorof c));
|
| % details of the level 1 components
| TOP.Name = T;
| TOP.Level = 1;
|
| NODE.Name = Node;
| NODE.Level = 1;
| NODE.Role in ran node;
|
| ARC.Name = Arc;
| ARC.Level = 1;
| #(arc~(ARC.Role)).Terminals = 0;
|
| ISA.Name = IsA;
| ISA.Level = 1;
| GetTerminal(ISA,1) = TOP;
| GetTerminal(ISA,2) = TOP;
|
| CONTEXT.Name = Context;
| CONTEXT.Level = 1;
| members~((node~(CONTEXT.Role)).Contents) = {}; %CONTEXT has no members
|
| % the type hierarchy for the level 1 components
| TOP->UniversalOntology parentof NODE;
| TOP->UniversalOntology parentof ARC;
| ARC->UniversalOntology parentof ISA;
| NODE->UniversalOntology parentof CONTEXT;
|
| % The only level 1 objects are TOP, NODE, ARC, ISA, and CONTEXT and their
| % isa arcs that define the type hierarchy
| #{c:COMPONENT | c.Level = 1} = 9;
|
| % there are no cycles over the isa relationship
| forall c:Contents @ not (c->UniversalOntology ancestorof c);
|
| % everything is a NODE or ARC, but only one of these
| forall c:Contents @
| (c->UniversalOntology isa NODE \/ c->UniversalOntology isa ARC) /\
| (c->UniversalOntology isa NODE) => not (c->UniversalOntology isa ARC)/\
| (c->UniversalOntology isa ARC ) => not (c->UniversalOntology isa NODE);
|
| % CONTEXTs contain only other objects in the graph
| forall x:CONTEXT_COMPONENT | x in Contents @
| forall m:COMPONENT | m incontext x @ m in Contents;
------------------------------------------------------------------------
Requirement 15 necessitates a mechanism to constrain components. For example, arcs need to be constrained so that they can't terminate on themselves. Validators act as constraint rules attached to components. A Validator is merely a boolean function applied to a Component in the context of a graph. Since these constraints will apply to all subtypes (as defined by ISA_COMPONENT, below), it is necessary to use two Components as arguments - the first is the exact object under inspection, and the second is the supertype that actually contains the validator. In general, in the implementation, it is expected that actual validators would be function objects (Laufer 1995; Nelson 1995).
VRES ::= PASS | FAIL VALIDATOR == COMPONENT & COMPONENT & GRAPH0 & OFilter --> VRES
The remainder of this section lists a few specific VALIDATORs that will be needed shortly. Their definitions follow.
No arc may refer to itself. This rule will be added to the definition of an ARC.
| NoSelfReference: VALIDATOR |-------------- | forall apply, owner: ARC_COMPONENT; g: GRAPH0; o:OFilter | | apply in g.Contents /\ owner in g.Contents @ | NoSelfReference(apply,owner,g,o) = | if (forall t:second(| (arc~(apply.Role)).Terminals |) @ | apply /= t.Anchor) | then PASS | else FAIL
The following VALIDATOR template restricts the arity of an arc. It is actually a function that takes a positive integer argument and returns a VALIDATOR that restricts the arity to be equal to the value of the argument. This can be easily implemented as a C++ function object (with state - the argument). Similar functions could easily be defined for greater-than, less-than, etc. Implementations should contain these in a validator library.
| ArityEquals: N1 --> VALIDATOR |--------------- | forall n: N1 @ | ArityEquals(n) = (mu v:VALIDATOR | | forall apply, owner: ARC_COMPONENT; g: GRAPH0; o:OFilter | | apply in g.Contents /\ owner in g.Contents @ | v(apply,owner,g,o) = | if (#((arc~(apply.Role)).Terminals) = n) | then PASS | else FAIL)
The Directed VALIDATOR specifies a binary from-to arc. This will be used to restrict the isa arc (Requirement 8).
| Directed: VALIDATOR |-------------- | forall apply, owner: ARC_COMPONENT; g: GRAPH0; o:OFilter | | apply in g.Contents /\ owner in g.Contents @ | Directed(apply,owner,g,o) = | if (ArityEquals(2)(apply,owner,g,o)=PASS /\ | GetTerminalDir(apply,1) = FROM /\ | GetTerminalDir(apply,2) = TO) | then PASS | else FAIL
The Upward VALIDATOR is a specialization of the Directed VALIDATOR that must be from an object at a level lower or equal to the level of the to side. Also, the level of the isa arc itself must be the same as that of the from side.
| Upward: VALIDATOR |-------------- | forall apply, owner: ARC_COMPONENT; g: GRAPH0; o:OFilter | | apply in g.Contents /\ owner in g.Contents @ | Upward(apply,owner,g,o) = | if (Directed(apply,owner,g,o)=PASS /\ | (GetTerminal(apply,1)).Level >= (GetTerminal(apply,2)).Level /\ | apply.Level <= (GetTerminal(apply,1)).Level) | then PASS | else FAIL
An arc cannot refer to anything outside the graph it is contained in. This validator is related to the NoDanglingTerminals validator but allows dangling terminals and explicity checks for graph membership. (NoDanglingTerminals does not.)
| ConfinedToGraph: VALIDATOR
|--------------
| forall apply, owner: ARC_COMPONENT; g: GRAPH0; o:OFilter |
| apply in g.Contents /\ owner in g.Contents @
| ConfinedToGraph(apply,owner,g,o) =
| if (forall i:N | i<=#(arc~(apply.Role)).Terminals @
| GetTerminal(apply,i) in (g.Contents || {NULLCOMPONENT}))
| then PASS
| else FAIL
A component cannot override a CONSTANT attribute (Requirement 22).
| NoConstAttrOverrides: VALIDATOR |-------------- | forall apply, owner: COMPONENT; g: GRAPH0; o:OFilter | | apply in g.Contents /\ owner in g.Contents @ | NoConstAttrOverrides(apply,owner,g,o) = | if (forall a:apply.Attributes @ | not (exists c2:g.Contents | (c2->o)->apply in g.ancestorof0 @ | forall a2:c2.Attributes | a2.Name = a.Name @ CONSTANT in a2.Flags)) | then PASS | else FAIL
Arcs must conform to their parents' arcs; that is, the child's arity must be greater than or equal to the arity of the parent, and all terminating objects in the child must be sub-types (or equal) of the corresponding (and non-missing) types of the parent's terminating objects. This restriction is a corollary of Requirement 14.
| ArcConformance: VALIDATOR |-------------- | forall apply, owner: ARC_COMPONENT; g: GRAPH0; o:OFilter | | apply in g.Contents /\ owner in g.Contents @ | ArcConformance(apply,owner,g,o) = | if (forall c2:ARC_COMPONENT | c2 in g.Contents /\ | (c2->o)->apply in g.ancestorof0 @ | % subtypes must have equal or more terminals | #(arc~(c2.Role)).Terminals <= #(arc~(apply.Role)).Terminals /\ | % subtypes must type-conform at each terminal | (forall i:Z | i<=#(arc~(c2.Role)).Terminals @ | (GetTerminal(apply,i)->o)->GetTerminal(c2,i) in g.isa0)) | then PASS | else FAIL
Contexts are strictly nested and no component may be a member of more than one context (Requirement 12). Note that the previous statement is a bit redundant: since contexts are themselves components, it is sufficient to say no component may be a member of more than one context. This rule will be added to the definition of a CONTEXT.
| NestedContexts: VALIDATOR |-------------- | forall apply, owner: CONTEXT_COMPONENT; g: GRAPH0; o:OFilter | | apply in g.Contents /\ owner in g.Contents @ | NestedContexts(apply,owner,g,o) = | if (forall c:g.Contents @ | % no component is a member of more than one context | c in members~((node~(apply.Role)).Contents) => | (forall c2:CONTEXT_COMPONENT | c2 in g.Contents /\ c2 /= apply @ | not(c in members~((node~(c2.Role)).Contents)))) | then PASS | else FAIL
All isa arcs must have a filter that is a subset of each of its supertype isa arcs. The restriction is necessary to support Requirement 18, overlayed type lattices.
| IsaSubtypesHaveSmallerFilters: VALIDATOR |-------------- | forall apply, owner: ISA_COMPONENT; g: GRAPH0; o:OFilter | | apply in g.Contents /\ owner in g.Contents @ | IsaSubtypesHaveSmallerFilters(apply,owner,g,o) = | if (forall p:ISA_COMPONENT | | p in g.Contents /\ (p->UniversalOntology)->apply in g.ancestorof0 @ | GetFilter(apply) subseteq GetFilter(p)) | then PASS | else FAIL
An arc with the NoDanglingTerminals contraint must have all its terminals linked to a valid object in the graph (none can be uninstantiated or "dangling"). Natureally, this constraint applies to all isa arcs. Note that this is related to the ConfinedToGraph validator: ConfinedToGraph allows dangling terminals while this constraint does not. Also, NoDanglingTerminals does not explicitly check for membership in the graph.
| NoDanglingTerminals: VALIDATOR |-------------- | forall apply, owner: ARC_COMPONENT; g: GRAPH0; o:OFilter | | apply in g.Contents /\ owner in g.Contents @ | NoDanglingTerminals(apply,owner,g,o) = | if (forall i:N | i<=#(arc~(apply.Role)).Terminals @ | GetTerminal(apply,i) in g.Contents) | then PASS | else FAIL
The following validator is not required by the specification, but it serves as an example of how to restrict graphs in ways that are commonly required by various graphical formalisms.
NoArcBtwnArcs disallows arcs between arcs (except ARC itself and all ISA arcs). This validator can be used at the ARC level to force first order graphs.
| NoArcBtwnArcs: VALIDATOR |-------------- | forall apply, owner: ARC_COMPONENT; g: GRAPH0; o:OFilter | | apply in g.Contents /\ owner in g.Contents @ | NoArcBtwnArcs(apply,owner,g,o) = | if (((apply->o)->g.ARC in g.isa0 /\ apply /= g.ARC /\ | not((apply->o)->g.ISA in g.isa0)) => (forall t:TERMINAL | | t in ran (arc~(apply.Role)).Terminals @ | (t.Anchor->o)->g.NODE in g.isa0)) | then PASS | else FAIL
Now that validators have been specified and several instances of validators have been defined, a TYPED_GRAPH can be described. A typed graph has several constraints over GRAPH0:
All of the above rules are applied as constraints (VALIDATORS) on the four basic components in the graph. Furthermore, all these validators must be satified for every subtype of the four basic components; and since everything is a subtype of one or two of these, the entire graph is appropriately constrained.
---TYPED_GRAPH-----------------------------------------------------------
| GRAPH0;
|-------------
| % T restrictions
| {NoConstAttrOverrides} subseteq TOP.Constraints;
|
| % arc restrictions
| {NoSelfReference, ConfinedToGraph, ArcConformance}
| subseteq ARC.Constraints;
|
| % an isa arc is binary upward-directed arc (recall that ISA isa ARC, and
| % "inherits" its constraints)
| {Upward, NoDanglingTerminals} subseteq ISA.Constraints;
|
| % context restrictions
| {NestedContexts}
| subseteq CONTEXT.Constraints;
|
| % all components satisfy their constraints
| exists g:GRAPH0 | g.Contents = Contents @
| forall c,p:g.Contents | (c->UniversalOntology) isa p @
| (forall s:paths_btwn(c,p,UniversalOntology) @
| forall v:VALIDATOR | v in p.Constraints @
| v(c,p,g,second(first(s(#s)))) = PASS)
| /\
| (forall v:VALIDATOR | v in c.Constraints @
| v(c,c,g,UniversalOntology) = PASS)
|
--------------------------------------------------------------------------
The following is a consistency corollary of the above TYPED_GRAPH schema and can easily be proved from it. Every component is the same top-level type as all of its supertypes.
forall g:TYPED_GRAPH @ forall c1,c2:g.Contents | (c1->UniversalOntology)->c2 in g.isa0 @ (c1->UniversalOntology)->g.NODE in g.isa0 <=> (c2->UniversalOntology)->g.NODE in g.isa0 /\ (c1->UniversalOntology)->g.ARC in g.isa0 <=> (c2->UniversalOntology)->g.ARC in g.isa0
This section lists operators on graphs.
The following functions determine the value of a particular attribute given a TYPED_GRAPH, a component, and an attribute name. The first function, getAttr searches for an attribute - looking first in the actual component, then attempts to select the highest priority attribute that is not hidden by an intervening attribute. Note that locked attributes are already taken care of in the TYPED_GRAPH schema. Note also that this function is not necessarily deterministic: this problem will have to be addressed in the future.
GETATTR_RESULT ::= Attr<> | NULLr
| getAttr: TYPED_GRAPH & COMPONENT & ATTRIBUTE_NAME --> GETATTR_RESULT
|--------------
| forall g:TYPED_GRAPH; c:COMPONENT; a:ATTRIBUTE_NAME | c in g.Contents @
| getAttr(g,c,a) =
| if a in {a1:ATTRIBUTE_NAME | exists at:c.Attributes @ a1 = at.Name}
| % c actually has the attribute
| then (mu x:c.Attributes | (a = x.Name))
| else if {x:GETATTR_RESULT |
| forall c2:g.Contents |
| (c2->UniversalOntology)->c in g.parentof0 @
| x=getAttr(g,c2,a)} = {}
| % attribute not found
| then NULLr
| % attribute found in one of the ancestors:
| else (mu x:ATTRIBUTE | forall c2:g.Contents |
| (c2->UniversalOntology)->c in g.parentof0 /\
| (exists y:ATTRIBUTE @ y=Attr~(getAttr(g,c2,a))) @
| exists y:ATTRIBUTE | y=Attr~(getAttr(g,c2,a)) @
| forall c3:g.Contents |
| (c3->UniversalOntology)->c in g.parentof0 /\
| (exists z:ATTRIBUTE @ z=Attr~(getAttr(g,c3,a))) /\
| (not ((c3->UniversalOntology)->c2 in g.ancestorof0)) /\
| (not ((c2->UniversalOntology)->c3 in g.ancestorof0)) @
| exists z:ATTRIBUTE | z=Attr~(getAttr(g,c3,a)) @
| y.Priority<=z.Priority /\ x=y)
The getValue function is similar to the above function, but simply returns a value if one can be found.
GETVALUE_RESULT ::= Val<> | NULLv | getValue : TYPED_GRAPH & COMPONENT & ATTRIBUTE_NAME --> GETVALUE_RESULT |--------------- | forall g:TYPED_GRAPH; c:COMPONENT; a:ATTRIBUTE_NAME | c in g.Contents @ | getValue(g,c,a) = if getAttr(g,c,a)=NULLr | then NULLv | else (Attr~(getAttr(g,c,a))).Value
setAttr takes a component and an attribute and merely adds the attribute to the component's set of attributes, replacing any attributes whose name might have matched.
---setAttr----------------------------------------------------------------
| Delta TYPED_GRAPH;
| c?: COMPONENT;
| attr?: ATTRIBUTE
|---------------
| c? in Contents;
| Contents' = (Contents \ {c?}) || {(mu c2:Contents |
| c2.Name = c?.Name /\
| c2.Level = c?.Level /\
| c2.Role = c?.Role /\
| c2.Attributes = (c?.Attributes \
| {a:c?.Attributes | a.Name = attr?.Name}) ||
| {attr?})}
--------------------------------------------------------------------------
Its a simple procedure to add a node to a graph:
---addNode----------------------------------------------------------------
| Delta TYPED_GRAPH;
| node?: NODE_COMPONENT;
| type?: NODE_COMPONENT;
| o?: OFilter;
|---------------
| TYPED_GRAPH';
| type? in Contents;
| not (node? in Level1Objects);
| Contents' = Contents || {node?, (mu a:ISA_COMPONENT |
| GetTerminal(a,1)=node? /\ GetTerminal(a,2)=type? /\ GetFilter(a)=o?)};
--------------------------------------------------------------------------
Note that, due to the invariants on the graph, the node cannot have any non-ISA arcs in the graph that refer to it immediately after its insertion. Note also that, by virtue of the definition of NODE_COMPONENT, the new node is a subtype of NODE (and therefore there exists an chain of ISA links from the new node to NODE.
It is just as simple to add a new arc:
---addArc-----------------------------------------------------------------
| Delta TYPED_GRAPH;
| arc?: ARC_COMPONENT;
| type?: ARC_COMPONENT;
| o?: OFilter;
|---------------
| TYPED_GRAPH';
| type? in Contents;
| not((arc?->UniversalOntology) isa ISA);
| not(arc? in Level1Objects);
| Contents' = Contents || {arc?, (mu a:ISA_COMPONENT |
| GetTerminal(a,1)=arc? /\
| GetTerminal(a,2)=type? /\
| GetFilter(a)=o?)};
--------------------------------------------------------------------------
But note that there is more going on here than meets the eye. Because of the constraints on a typed graph, the arc must refer only to nodes that are already members of the graph contents.
It must also be possible to change the type of node or arc. However, since this system uses multiple inheritance, "changing" the type makes little sense. Instead, one can set an object to be some type (by adding an isa-arc). Removing a type from a component's set of parent types is just a matter of deleting a particular isa arc and can be accomplished by using remove, as shown below.
---setComponentType-------------------------------------------------------
| Delta TYPED_GRAPH;
| c?: COMPONENT;
| newType?: COMPONENT
|---------------
| TYPED_GRAPH';
| ((c?->UniversalOntology) isa NODE /\
| (newType?->UniversalOntology) isa NODE) \/
| ((c?->UniversalOntology) isa ARC /\
| (newType?->UniversalOntology) isa ARC );
| c? in (Contents \ Level1Objects);
| newType? in Contents;
| Contents' = Contents ||
| {(mu a:ISA_COMPONENT | GetTerminal(a,1)=c? /\
| GetTerminal(a,2)=newType?)};
--------------------------------------------------------------------------
Removing any component from a graph entails removing all references to it from arcs (including isa arcs) and contexts. One problem is that if the removed node was a supertype of some existing component, then the subtype component will be left with a dangling isa chain. This is prevented by disallowing it in precondition.
---remove-----------------------------------------------------------------
| Delta TYPED_GRAPH;
| c?: COMPONENT;
|---------------
| TYPED_GRAPH';
| c? in (Contents \ Level1Objects);
| not (exists c2:Contents @ (c2->UniversalOntology) isa c?);
| % the target is removed
| Contents' = Contents \ {c?};
| % either arcs are dangling or removed
| forall a,oa:ARC_COMPONENT |
| oa in Contents /\ a in Contents' /\ a.Name=oa.Name @
| forall i:N @ GetTerminal(oa,i)=c? => GetTerminal(a,i)=NULLCOMPONENT;
| % the removed component is deleted from any enclosing context
| forall cxt,ocxt:CONTEXT_COMPONENT |
| c? incontext ocxt /\ ocxt.Name=cxt.Name @
| not (c? incontext cxt);
--------------------------------------------------------------------------
It is not particularly common in visual graph languages to allow arcs between arcs, and this restriction may easily be applied to this typed graph theory. Such a graph is called a FIRST_ORDER_TYPED_GRAPH, and is just a constraint on an ordinary TYPED_GRAPH: all arc terminals must refer to nodes only. Note that this does not constrain the type system, as isa arcs can refer to nodes or links (or other isas).
%% state-schema FIRST_ORDER_TYPED_GRAPH
FIRST_ORDER_TYPED_GRAPH =^= [TYPED_GRAPH |
{NoArcBtwnArcs} subset ARC.Constraints
]
This schema demonstrates just how simple it can be to constrain a graph to a particular syntax.
This chapter has described the specification of the Constraint Graphs system. The Constraint Graphs system consists of a TypedGraph which acts as container of graph COMPONENTs. A Typed Graph also has the responsibility to maintain various invariants among its components. Every graph component has a name, a level, a set of attributes and a set of constraints. There are four types of components: nodes, contexts, arcs, and isa arcs. Attributes are named values where the type of the value is left open; however, while the value of an attribute can be overridden when it is inherited, its type cannot be changed.
The specification given in this chapter is a clear and unambiguous description of the theory and the framework and supports Objective 1 and Objective 2. This is an important result of the specification, but equally important, the specification was used during the development of the theory to work with the various possible variants before committing to an implementation. The cost of backtracking to design during the implementation stage is often prohibitively expensive (so it not always done when it should be, compromising the software design). Working with the specification, and ironing out as many problems as possible in the specification minimizes the commitment to a particular design, encourages backtracking to design, and therefore can lead the a better final design. During development, several inconsistencies and possible generalizations were detected at the specification stage; the minimal commitment at this stage made it easy to backtrack to the preliminary design to correct the errors. For example, early versions of the theory had a much less clean fundamental type lattice (isa was not originally a subtype of an ordinary arc), but the specification made the similarities and the (now-obvious) subtype relationship clear, and this observation was propagated back into an improved theory. Many iterations of the specification lead to a much stronger theory and final design of the framework. The specification will continue to be used as pre-implementation testing ground for framework design and theory changes.
The drawback of the specification is the time and effort it takes to produce a specification. The process of creating a specification can involve nearly the effort it takes to produce a prototype-level implementation. This is particularly true when the specification language is not a perfect match for the domain (as happened with the Z language and the convoluted way in which one has to specify inheritance relationships – see the introduction to this chapter). However, for a research area in which the direction is not clear, the clarity and unambiguous nature of the specification seems well worth the effort (as it was in this case).
This chapter does not describe the interface
or any kind of user interaction. That is separate layer, and
is discussed in the next chapter.
 Chapter 4
Chapter 4
 index
index
 Chapter 6
Chapter 6
 Constraint Graphs: A Concept Map Meta-Language (PhD Dissertation), Department of Computer Science
Constraint Graphs: A Concept Map Meta-Language (PhD Dissertation), Department of Computer Science