 Rob Kremer
Rob Kremer

 Chapter 3
Chapter 3
 index
index
 Chapter 5
Chapter 5
Although the presentation of the requirements in this chapter makes it appear that the requirements were developed before the specification and software were begun, this is not the case. Like most software development efforts, the detailed design, implementation, and testing stages uncovered further requirements that were not apparent during the initial analysis. For example, until it was found that individuals' visual attribute inheritance from concepts lead to some unexpected properties in implementing the KDraw language, the designer was unaware of the need for multiple type lattices. At that point the requirements were revisited to add Requirement 18 to the list of requirements: the new requirement was woven into the specification, and the new feature was added to the implementation.
The requirements were first derived by studying several concept mapping languages – KDraw and Conceptual Graphs were first studied before the specification and implementation were begun. Once the first working implementation was produced, Constraint Graphs was tested by applying it to the definition of other languages such as gIBIS and several object oriented design languages. Although these tests produced no significant changes to the requirements (probably owing to their relative simplicity compared to knowledge representation languages), more detailed implementations of the original two languages, KDraw and Conceptual Graphs, produced some very interesting results. For example, a reformulation of the implementation of Conceptual Graphs to take advantage of arc constraints could yield a much more powerful system with considerable semantics checking (see Section 7.2). In addition, the post-implementation detailed implementation of KDraw, adding visual attribute inheritance from concepts, produced some unexpected new requirements as mentioned above.
There is no reason to believe that the set of requirements listed here will remain static. But rather, it is expected that the requirements (and the theory) should evolve dynamically over time – as more and more languages are implemented under Constraint Graphs.
The basic objective of this work is to develop a concept map framework under which one may easily build various formal and informal visual knowledge representation notations.
| Develop a general and flexible concept map framework for visual knowledge representation. |
Ideally, one should be able to create new graphical knowledge representation languages in a recursive fashion by using concept maps themselves to specify the features in the new language. An obvious corollary is that the framework should be able to imitate existing knowledge representation languages, and this is where most of the emphasis will be placed, since it avoids the trap of creating a language with features specific to a particular model. Examples of knowledge representation languages to be captured by this framework are Gaines' KDraw (Gaines 1991b) and Sowa's Conceptual Graphs (Sowa 1984).
Since this objective emphasizes generality and flexibility, it is also appropriate to choose examples of graphical, semi-formal, non-knowledge representation languages to generalize the test applications. Examples of such languages are gIBIS (Conklin & Begeman 1987) for decision support and Object Model Notation (Coad, North & Mayfield 1995) for object-oriented program design.

The objective does not imply that the implementation is intended to exactly match the target visual languages. For example, Object Model Notation uses nodes with three distinct sections (see Figure 10); for the purposes of this implementation it will be considered adequate to simplify by avoiding the double border and use semicolons in place of the separator lines.
On the other hand, certain natural extensions to existing notations should be considered appropriate for the implementation. For example, Conceptual Graphs rely on an associated semantic net, composed in a separate notation, to specify the type lattice. The examples in Sowa's 1984 book (Sowa 1984) use the textual notation in the appendix as their associated semantic net. For the purposes of this work, it is a reasonable (and compelling) extension to allow both the Conceptual Graph and semantic net to be combined in the same graph.
Since this work is intended to be a framework used as the base for other systems and as a model for the theory, the structure of its design must be very clear and unambiguous. One appropriate path to this end is to use formal methods, since formal methods will provide a logically precise design and serve as a reference point to resolve ambiguities. However, software engineering principles dictate that wholesale application of formal methods may be inappropriate since over-application of formal methods will increase the required effort of the project beyond reasonable levels (DeMarco 1982). The "engine" component of the framework is deemed appropriate for formal specification, while the user interface is viewed as an add-on (replaceable) component that would be inappropriate to formally specify. It is the engine component of the framework that models the theory and needs to be unambiguous and rigorous if it is to show its accurate modeling of the theory.
|
| The design should be formal and rigorous where appropriate. |
Formal methods will be used for the core parts of this work that are most subject to ambiguous interpretation. This does not imply that the rest of the work should be done haphazardly: the entire work, from design to coding should be done a principled way. Both the parts that are formally specified and the parts that are not should be properly designed, documented, and coded taking advantage of standard class libraries and techniques. A clear and principled design and development process will contribute to the confidence in the accurate correspondence between the software framework and the theory.
|
| The target system should be developed in a principled manner. |
A recent approach to principled software development is the explicit use of design patterns (Gamma et al. 1995; Pree 1995), which provide detailed, semi-formal documentation of design concepts that have proven track records in past projects. One of the advantages of design patterns is that they provide a vocabulary and starting point for design, and many of them can be encoded as general-purpose classes in object-oriented class libraries.
In addition, this work should take full advantage of existing principled tools. For example, the C++ Standard Template Library (STL) (Nelson 1995; Stepanov & Lee 1995), is a container library which has been developed and documented in a principled way.
The first requirement is that there must be a clear separation between the part of program that enforces the rules of layered visual languages (the constraint graph) and the part that implements the visual graphics and accepts user commands (the user interface).
| The system should have a clear separation between the constraint graph engine and the user interface. |
This requirement addresses Objective 1 (flexibility and generality) by allowing configurations with differing constraint graph engines and user interface engines. Such a design yields high flexibility and generality. A monolithic system may not be sufficiently flexible. This requirement also supports Objective 3 (principled development).
As an example, one might consider the choice of implementation languages. The constraint graph system and the user interface system differ in their computation attribute considerably: The constraint graph sub-system is likely be to quite computationally complex (since it is known many type systems have polynomial or exponential complexity), while the user interface sub-system (graphical drawing) is not likely to be a computational bottleneck because the reasonably simple drawing operations are very fast compared to the interaction rate of the human user. Furthermore, the constraint graph sub-system, since it has nothing to do with the user interface, is likely to be easily portable between operating systems (if written in a reasonably portable language), while the user-interface is not likely to be easily portable between operating systems because its many graphical input/output operations will be implemented quite differently on the different operating systems. The two parts of the program differ in computational complexity and in ease of porting to another operating system. C or C++ would be a reasonable language choice to address the computational complexity of constraint graph sub-system, but, on the other hand, the limited portability of user interface libraries does not address the concerns of the user interface sub-system. Java is a cross-platform portable language, which addresses the user interface sub-system, but, on the other hand, it is relatively slow, and will not perform well as the language of the constraint graph sub-system. Since the two sub-systems differ remarkably in their feature profiles, it may make good sense to implement them in different languages. Only a clean separation between the two will yield the flexibility to do this.
A Constraint Graph is defined here as a very abstract graph, in the graph-theoretic sense, that contains the usual nodes and arcs. In addition, it enforces a strict typing on the nodes as defined by a special arc type, called isa. Several other forms of constraints are also applied, as detailed below, in order to satisfy Objective 1, a framework in which to emulate and experiment with visual knowledge representation systems.
The Constraint Graph itself will have no user interface of its own (see Requirement 1). However it will have an interface to other programs that can implement an interface on its behalf.
Many graphical knowledge representation systems, whether formal or informal, use separate and/or non-graphical notational mechanisms to represent the type lattice of graphical components. Two examples are Accord (Kremer 1993), which uses a complex dialog box to edit its type hierarchy; and Conceptual Graphs (Sowa 1984), which uses a separate and distinct semantic net to present its type lattice. This is not unexpected: there is a firm distinction between types and objects. In philosophy, Zalta (1988; 1993) defines abstract objects (types) as encoding properties and ordinary objects (objects) as exemplifying properties. But there are many definitions of types and objects (see Section 3.1), depending on one's perspective.
On the other hand, other languages such as CLASSIC (Borgida et al. 1989) and KDraw (Gaines 1991b3) cleanly integrate the ontology (type relationships) graph with the domain graph. This makes for a clean and clear representation of knowledge without forcing the user to learn several different tools or sub-formalisms.
Constraint Graphs should cleanly integrate ontology and domain data in a single graph.
| Ontology graphs should be cleanly integrated with domain graphs. |
This integration is necessary to support integrated languages like KDraw. Furthermore, it does no damage in representing languages like Conceptual Graphs because the ontology is a clean "add-on" that can be ignored by traditionalists. Requirement 2 supports Objective 1.
In the case of Constraint Graphs, where the objectives include both flexibility and rigor, one must be very careful. In many cases, the user will require Zalta's rigorous distinction between type (astract objects) and objects (ordinary objects); but in other cases this rigor may be damaging to the flexible support of multiple visual languages. For example, one may build up layers of ontologies upon one another. It is not always clear to the user which is a type and which is an object; it depends on the user's perspective. For example, one may have a "universal" ontology (representing "thing", "physical_thing", "intangible_thing", etc.), and use the universal ontology as the basis for an ontology of machines, and use the machine ontology as the basis for an ontology about photocopy machines, and use the photocopy machine ontology as the basis for an ontology about the Xerox-9000 line of photocopy machines, and finally use the Xerox-9000 ontology as the basis for a domain graph about specific photocopy machines on the third floor of the library. Each successive ontology behaves as though it were a domain based on the ontology above it. Furthermore, although the chain of ontologies appears to terminate with the specific machines, this is not necessarily the case. One could use the specific photocopy machine domain as an ontology for a domain about the machine variants caused by engineering updates to the machines (where the type changes over time, but not identity).
Another case where the distinction of type and object becomes blurred is in dealing with metaclasses. A class defines the properties of an object, but a metaclass defines the properties of a class. For example, the metaclass might define a superclass, a name identifier, a list of attributes, and a list of methods.
The point is that Constraint Graphs needs to use a typing system with a great deal of flexibility: there isn't always a clear distinction between type/class/concept and instance/object/individual, and some entities may have to viewed sometimes as an type and sometimes as an instance.
This notion of not clearly recognizing the distinction between type and instance may seem somewhat heretical, but it is not without support in other systems. Object-based languages do not contain the notion of class, but many of these languages can support a form of inheritance through prototypes (fully functional objects used to "template" new objects) and either embedding or delegation (see Section 3.1.1). Abadi and Cardelli (1996) make a very good argument that "objects are more primitive than classes and should be understood and explained before classes" (p. 49) and that classes arise out of objects. Furthermore Lieberman (1986) shows that delegation is more powerful than class-based inheritance.
It therefore makes good sense in Constraint Graphs to refuse to recognize as primitive the differences between type and instance:
| The system should enforce no intrinsic distinction between types and instances. |
If a system needs to distinguish between types and instances (as in KDraw's concepts and individuals) one can do it by tagging a parent type of the "instances" with a constraint (see Requirement 15) such as "no subtype may itself have any subtypes"
A good rule-of-thumb for any software engineering project (and for any undertaking whatsoever) is "keep it simple". It follows that the base type system for Constraint Graphs should be as simple and succinct as possible.
Graph theory dictates that at least a node type and an arc type are required. Node and arc are mutually exclusive. Since type theory is also supported, a means to represent the type hierarchy is also required. This can easily be accomplished by using a specialized directed arc type called isa, which is, itself, a subtype of arc.
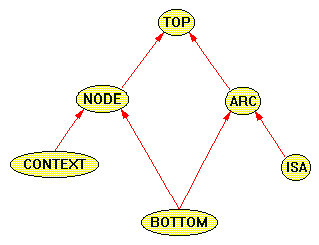
In addition, some mechanism for grouping and nesting is required. Conceptual Graphs uses contexts to group sub-graphs into "possible worlds". Examples of Conceptual Graphs contexts are NEGATION, PROPOSITION, and SCENE. Contexts are strictly nested, and so form a hierarchy of sub-graphs. While contexts are not used in CLASSIC, they are used in KDraw (which is based on CLASSIC) as a useful visual aid to the user (there is no associated semantics). Since contexts are used exactly as nodes in Conceptual Graphs, contexts should be a subtype of the node type. One could argue that contexts are related to arcs since they "connect" or group other objects, but this argument is not sound because arcs form ordered collections and have no hierarchy, while contexts form unordered collections and are hierarchical (see Section 4.3.2.4). The base type lattice for Constraint Graphs is given in Figure 11.
|
| The base type lattice should be "context < node < top > arc > isa", where node and arc are mutually exclusive. |
In mapping from Conceptual Graphs to Constraint Graphs, Conceptual Graphs' relations map to Constraint Graphs' arcs quite naturally. (One could also map relations onto nodes and make special bipartite rules.) Since Conceptual Graphs relations are of arbitrary arity (but not zero), Constraint Graphs is compelled to make arcs have arbitrary arity. See also Section 3.2.1.
| Arcs are n-ary, but must have arity greater than zero. |
While binary arcs are by far the most common in visual languages, Sowa (1984) makes compelling arguments to support n-ary relations. For example the between relation is very hard to represent using only binary arcs. Ordered lists can also be conveniently represented as open-ended n-ary arcs.
Many visual languages contain directed as well as undirected arcs. Both types can be easily simulated by keeping the terminals of arcs ordered.
| Arc's terminals are ordered. |
Many visual languages are "first-order" (drawing a parallel to predicate calculus) in that they allow arcs only between nodes (and not other arcs). But some visual languages are "higher-order" in that they do allow arcs between arcs. This dictates that Constraint Graphs must support arcs between arcs.
| Arcs may terminate on objects of type node or arc. |
This feature is also used to form a type lattice of arcs (Requirement 9) which serves to restrict arc terminals (Requirement 14).
It has already been established that isa is a subtype of arc. But the semantics of isa still needs to be specified. Isa arcs are directed, binary arcs. (The "directed" part comes for free since arc terminals are ordered as per Requirement 6.) Isa arcs are constrained to be binary since there is no semantic difference between a component inheriting from two supercomponents via a single (trinary) isa arc, and inheriting from the same two supercomponents via two distinct (binary) isa arcs. Allowing higher-arity isa arcs only introduces unnecessary redundant methods and complicates specification and implementations.
| Isa arcs are strictly binary. |
One should be able to just "draw" in an isa arc between two objects to establish the subtype/supertype relationship between them. The type system should work on the basis of isa arcs, and either accept or reject modifications based on the lattice formed by the isa arcs (including the insertion and deletion of isa arc).
| The subtype/supertype relationship is established by drawing isa arcs between objects. The type system accepts or rejects graph modification based on the lattice of isa arcs within the graph. |
Contexts are specializations of nodes that "contain" subsets of the graph.
| Contexts are a subtype of node and so behave in the same manner as nodes. Arcs can terminate on contexts, as well as on objects contained within contexts. |
Contexts constitute partitions on a graph; that is, contexts represent subsets of the components of a graph. N-ary arcs may also be considered as representing graph partitions, but one must be careful to distinguish between n-ary arcs and contexts: contexts are set-like, so their referents are unordered with respect to the context; n-ary arcs are sequence-like, so their referents are ordered with respect to the arc.
| Contexts contain sub-graphs of the graph; the components of the sub-graph are unordered with respect to the context. |
Contexts form a strict hierarchy of subsets of a graph; they cannot overlap. This is in concurrence with Sowa's Conceptual Graphs. Logically, contexts differ from arcs in that they form a hierarchy, and objects they "refer to" form an unordered collection.
| Contexts are strictly nested: they form a hierarchy. |
One could argue that there is no inherent reason to make contexts hierarchical; after all, one of the objectives is to make the system as flexible as possible. It might make sense to allow partially overlapping contexts, then constrain partial overlaps away when necessary (as in the case of modeling Conceptual Graphs). Unfortunately, when one starts considering the physical layout of context boxes that contain subsets of each others' graphs, things quickly get out of hand. Two context boxes sharing a common sub-graph is not very difficult to draw, but the problem gets exponentially more difficult with more context boxes sharing arbitrary sub-graphs. For example, Vein diagrams work well for two or three sets, but the geometry gets increasingly difficult when one adds more sets. Even certain combinations of five sets are impossible to draw using contiguous two-dimensional shapes.
This Pandora's box is best avoided by simply conforming to Conceptual Graphs' hierarchical contexts. When sub-graphs must be shared between contexts, it can be done using coreference arcs as per Sowa's Conceptual Graphs.
In support of Objective 1, the design of Constraint Graphs must strive to be as flexible and powerful as possible in order to support representation of a large number of visual languages. It should also be easy to use.
|
| The graphical syntax of common visual languages should be implementable in the system without excessive low-level programming. |
The next two requirements are corollaries of Requirement 13.
The basic syntax of concept mapping languages is primarily concentrated on restricting the types of arcs that may be drawn between objects based on the objects' type. This can be accomplished naturally (and graphically) by use of the subtype relationship among arcs. As show in Section 3.2.2, arc types are covariant on the types of the nodes on which they may legally terminate. That is, any subtype arc may specialize the legal node type on which any of its terminals anchor. This may be reworded the other way around as Requirement 14:
| An arcs may terminate only on objects that are subtypes of the corresponding terminal in all the arc's supertypes. |
For example, in order to restrict the mother relationship arc to be between objects of person and type female-person, one only need create a prototype arc (from type person to female-person) and derive all mother arcs from this prototype. Figure 12 shows a simple ontology/domain describing the concepts person, female-person, and male-person together with the individuals Sally and Joe. Isa arcs are shown as unlabeled, directed, red arcs. A labeled binary directed arc is drawn from person to female-person (which is the prototype mothoer arc) to restrict the type of the terminal objects. Finally, a new arc of type mother (also labeled mother) is drawn between Joe and Sally. This arc is legal because Joe isa person and Sally isa female-person. The arc could not be drawn in the other direction because Joe does not have type female-person.
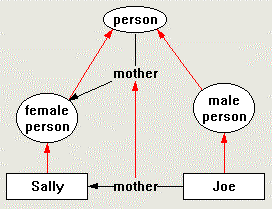
A problem may arise in the situation in Figure 12. Note that Requirement 14 talks about corresponding arc terminals, but does not restrict the addition of arc terminals (i.e., increasing the arity of an arc) in a subtype. This is as it should be. But occasionally one may want to restrict the arity of all subtypes of an arc. In the case of mother, this probably makes sense.
It turns out there are a large variety of restrictions that are necessary to emulate other visual languages. Some examples are:
To enumerate all of these possibilities is probably not possible for all conceivable visual languages. It makes sense to allow some mechanism for the user to easily extend the system to handle these cases.
| Some mechanism must exist to allow the user to "program" arbitrary constraints. These ad-hoc constraints could be collected in a library for easy use. |
The type system should be maintained at all times. That is, modifications to the graph should be disallowed if they violate constraints.
|
| Strong typing - all objects and types should conform to all their, and their supertypes' constraints. |
This means that whenever any object in the graph is modified, created, or deleted, the entire graph must be checked for constraint violations. In practice the entire graph does not have to be checked since there is a limit to the effect of a change. Changes will only affect objects below the changed object in the type lattice (subtypes), but all constraints of objects above each affected object (every supertype) will have to be checked against the affected objects. In addition, object modification will force constraint checks in their adjacent objects (for changed arcs, terminal objects; for all objects, the arcs that terminate on them). Requirement 15 (arbitrary constraints) can cause this constraint checking scheme to fail.
During the development of visual graphs there are always intervals where some part is inconsistent due to incompleteness. For example, while drawing a binary arc in single-step is an easy task (usually elastic line dragging), it is not so easy to draw a trinary arc in a single step. Instead, it makes more sense to allow the creation of the trinary arc with "dangling" terminals, and let the user "attach" the terminals as a separate operation.
The system must make some trade-off between always maintaining completeness and usability. Some constructs are not possible without temporary incompleteness or incorrectness. In general, simply allowing for dangling arc terminals is sufficient.
| The system should allow for incompleteness (e.g. dangling arcs) when the graph is in an intermediate state. |
Dangling arc terminals should always be considered a stand-in for an object of the correct type. In this respect, dangling arc terminals are analogous to null pointers in programming languages.
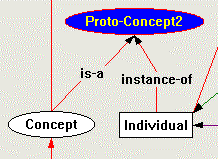
An interesting problem arrises when mapping KDraw to Constraint Graphs. In KDraw and CLASSIC ( Borgida et al. 1989) a distinction is made between concepts and individuals (unlike Constraint Graphs). The fact that individuals can't have subtypes is easily handled by a constraint (Requirement 15). But both the subtype (concept-to-concept) and instance-of (individual-to-concept) arcs seemed best modeled as subtypes of the base isa arc used by the Constraint Graphs' type system (see Figure 13). This allows an object of type individual to inherit attributes and constraints from its supertype concepts, as it should. But it also causes the individual to inherit properties (such as being the root of a has-rule arc) that violate the syntax of KDraw. Clearly, this indicates two separate (but closely related) type lattices superimposed on the graph. One of these lattices is the KDraw syntax and the other is the domain model. The two are exactly identical except that the instance-of arc is an isa arc in the domain model lattice, but not in KDraw syntax lattice.
|
| The system needs to support overlayed (but distinct) type lattices. Isa arcs can be tagged with the set of type lattices to which they apply. |
KDraw's individual/concept problem is solved using a filter on the subtypes of instance-of arcs to distinguish the two separate lattices. Isa arcs are tagged with the set of type lattices to which they apply. The type inference system can use the KDraw syntax ontology filter (which won't see the isa arc between an individual and a concept), while the attribute resolution system uses the domain model filter (which does see the isa arc between an individual and a concept).
Most isa arcs are tagged with the universal set.
In the interests of supporting an independent user interface (Requirement 1), the Constraint Graphs system must be able to cleanly carry information on behalf of the user interface. This information should be associated with the objects (nodes and arcs) in the graph. Furthermore, this information should be inherited by subtypes of objects. In short, the objects in the constraint graph need inheritable attributes with values. Inheritance is standard with almost any object oriented system, but specifically, this system uses delegate inheritance (see Section 3.1.1) which means that not only attributes and their types are inherited, but so are their values because the slot for the attribute is stored not in the host (subtype) but in the delegate (supertype). If attribute is not found in the host, it is searched for in the delegate(s). This is similar to inheriting a "default" value with the attribute, but the "default" can change if its changed in the parent.
|
| All objects in the graph will have associated attribute/value pairs that are inherited (delegated) through the type lattice. |
Delegation of attributes does not imply that an attribute value cannot be overridden. This is normally done by placing a slot in the host (subtype), thereby avoiding searching for the attribute in the delegate (supertype).
| Attributes and their values are inherited, but may be overridden. |
Although attribute values may be overridden, the attribute type may not be overridden or specialized in a subtype. Attributes that can be updated turn out to be invariant (neither covariant or contravariant). Abadi and Cardelli (1996) offer a proof based on pairs whose components can be updated (operator "$"):
If A<:A' and B<:B', can we covariantly allow A$B <: A'$B'? If we adopt this inclusion, then from p:A$B we obtain p: A'$B' and we can perform setLft(p,a') for any a':A'. After that, getLft(p) might return an element of type A' that is not an element of type A. Hence the inclusion AB <: A'$B' is not sound.
Conversely if A"$<:A and B"$<:B, can we contravariantly allow A$B<:A"$B"? From p:A$B we now obtain p:A"$B", and we can incorrectly deduce that getLft(p):A". Hence the inclusion A$B <: A"$B" is not sound either. (p. 21)
Requirement 21 is therefore necessary:
| Attribute values should be typed, and the attribute value type cannot be overridden by a subtype. |
It is also sometimes necessary to prevent a subtype from changing the value of an attribute. For example, in KDraw, a concept is always represented by an elliptical surround; to override this attribute would render the graph unreadable. Preventing overriding is analogous to the const tag in C and C++.
| It should be possible to prevent overriding of an attributes value. |
As discussed in detail for Requirement 2, there are usually several ontological levels; this is particularly true for as system such as Constraint Graphs where one has a base level (arcs and nodes), then defines a formalism (such as KDraw or Conceptual Graphs), then defines an ontology (or several levels of ontology), then defines a domain. It makes good sense to be able to group all the objects into their respective levels.
|
| Graph objects should be partitioned into ontological levels. |
The levels can then be used for various purposes. For example, the end user (the one who works on the bottom-level domain) does not often want to be concerned with anything but the lowest-level ontology. Therefore, choices the end user makes about type can be restricted to just that specific ontology level. Likewise, inferences the system makes about possible object typings can be restricted (and often completely disambiguated) by searching only in restricted levels.
Although the constraint graphs system is intended to be a formal system, it is also intended to be a useful and usable system. Usefulness and usability imply that the system must be able to handle situations in which users find it inconvenient or impossible to enter complete and correct graphs (Kremer 1994; 1995).
|
| Support for varying levels of formalization. |
While Requirement 17 addresses incompleteness, Requirement 24 is a more general statement which also encompasses incorrectness. One possibility for addressing this requirement is to allow the constraints (Requirement 15) to be tagged with an urgency value, which would allow the type system to violate constraints if the user so desired.
The user interface is not a central focus of this thesis, but it is critical to the usefulness and usability of this system. This section therefore briefly describes the requirements for a user interface to be used with the Constraint Graph system.
Besides the obvious requirement of being a flexible and extensible system that can call into the Constraint Graph system and receive update messages from it, the interface elements must conform to following list of requirements.
| Interface nodes should be labeled or unlabeled with little or no restriction on the characters in the label. |
| Interface nodes should have a reasonably rich set of visual attributes, including, but not restricted to, node shape, fill color, border color, and text color |
| Interface arcs must be able to be visually anchored to nodes, contexts and other arcs and to track them when they are moved. |
| Interface arcs should be labeled or unlabeled with little or no restriction on the characters in the label. |
| Interface arcs should have a reasonably rich set of visual attributes, including, but not restricted to, label shape, fill color, border color, and text color; line color; arrowhead style and color. |
| Interface arcs should have arbitrary arity. They must also have some method of visually distinguishing the order of the terminals. |
| Interface contexts should be labeled or unlabeled with little or no restriction on the characters in the label. They must be capable of visually containing subsets of the graph. |
| Interface contexts should have a reasonably rich set of visual attributes, including, but not restricted to fill color, border color, and text color. |
| There should be some mechanism in the interface were contexts may be restricted to be independent or nested, but not partially overlapped. |
This chapter has detailed the objectives and requirements of the Constraint Graph system. The primary objective is to produce a powerful and flexible system in which one can describe and implement a variety of visual language formalisms. The complete list of objectives is listed below:
| Develop a general and flexible concept map framework for visual knowledge representation. | |
| The design should be formal and rigorous where appropriate. | |
| The target system should be developed in a principled manner. |
The complete list of Constraint Graph requirements is listed below:
| The system should have a clear separation between the constraint graph engine and the user interface. | |
| Ontology graphs should be cleanly integrated with domain graphs. | |
| The system should enforce no intrinsic distinction between types and instances. | |
| The base type lattice should be "context < node < top > arc > isa", where node and arc are mutually exclusive. | |
| Arcs are n-ary, but must have arity greater than zero. | |
| Arc's terminals are ordered. | |
| Arcs may terminate on objects of type node or arc. | |
| Isa arcs are strictly binary. | |
| The subtype/supertype relationship is established by drawing isa arcs between objects. The type system accepts or rejects graph modification based on the lattice of isa arcs within the graph. | |
| Contexts are a subtype of node and so behave in the same manner as nodes. Arcs can terminate on contexts, as well as on objects contained within contexts. | |
| Contexts contain sub-graphs of the graph; the components of the sub-graph are unordered with respect to the context. | |
| Contexts are strictly nested: they form a hierarchy. | |
| The graphical syntax of common visual languages should be implementable in the system without excessive low-level programming. | |
| An arc may terminate only on objects that are subtypes of the corresponding terminal in all the arc's supertypes. | |
| Some mechanism must exist to allow the user to "program" arbitrary constraints. These ad-hoc constraints could be collected in a library for easy use. | |
| Strong typing - all objects and types should conform to all their, and their supertypes' constraints. | |
| The system should allow for incompleteness (e.g. dangling arcs) when the graph is in an intermediate state. | |
| The system needs to support overlayed (but distinct) type lattices. Isa arcs can be tagged with the set of type lattices to which they apply. | |
| All objects in the graph will have associated attribute/value pairs that are inherited (delegated) through the type lattice. | |
| Attributes and their values are inherited, but may be overridden. | |
| Attribute values should be typed, and the attribute value type cannot be overridden by a subtype. | |
| It should be possible to prevent overriding of an attribute's value. | |
| Graph objects should be partitioned into ontological levels. | |
| Support for varying levels of formalization. |
The complete list of interface requirements is listed below:
| Interface nodes should be labeled or unlabeled with little or no restriction on the characters in the label. | |
| Interface nodes should have a reasonably rich set of visual attributes, including, but not restricted to, node shape, fill color, border color, and text color. | |
| Interface arcs must be able to be visually anchored to nodes, contexts and other arcs and to track them when they are moved. | |
| Interface arcs should be labeled or unlabeled with little or no restriction on the characters in the label. | |
| Interface arcs should have a reasonably rich set of visual attributes, including, but not restricted to label shape, fill color, border color, and text color; line color; arrow head style and color. | |
| Interface arcs should have arbitrary arity. They must also have some method of visual distinguishing the order of the terminals. | |
| Interface contexts should be labeled or unlabeled with little or no restriction on the characters in the label. They must be capable of visually containing subsets of the graph. | |
| Interface contexts should have a reasonably rich set of visual attributes, including, but not restricted to fill color, border color, and text color. | |
| There should be some mechanism in the interface were contexts may be restricted to be independent or nested, but not partially overlapped. |
 Chapter 3
Chapter 3
 index
index
 Chapter 5
Chapter 5
 Constraint Graphs: A Concept Map Meta-Language (PhD Dissertation), Department of Computer Science
Constraint Graphs: A Concept Map Meta-Language (PhD Dissertation), Department of Computer Science