 Rob Kremer
Rob Kremer

 Chapter 2
Chapter 2
 index
index
 Chapter 4
Chapter 4
This chapter deals with the object oriented paradigm and specification. There is dual motivation for describing the object oriented paradigm: The graphical meta-language developed in this thesis is an object-based system, and the language implementation and design use the object oriented paradigm.
Several issues in the object oriented languages design space are covered as background to issues that arise later in the development of Constraint Graphs. These issues include the classification of object oriented languages into class-based and object-based languages, several different inheritance models, and covariance, contravariance, and invariance. Furthermore, concept maps, which have already been discussed in chapter 2 are revisited in this chapter in light of the inheritance and typing issues discussed here.
Finally, specification and the Z specification language are briefly introduced as background to chapter 5.
The object oriented paradigm is an important part of computer programming. To quote Abadi and Cardelli (1996) discussing the various programming paradigms:
"…the object-oriented approach has proven uniquely successful. It manages to integrate analysis, design, and implementation techniques into a relatively intuitive and uniform framework." (p. 8)There are a very large number of object oriented programming languages in existence today, with varying degrees of acceptance and use. There are several schools of thought on what constitutes an object oriented language; many of these schools would deny many of the others the label "object oriented". For example, the "strongly typed" school might deny that (untyped) Smalltalk is an object-oriented language at all. Most of the differences pivot on the use and the conceptualization of objects, classes, and types.
What is the difference between an object, a class and a type? There are many definitions. Thought on the subject goes back to at least Plato. However, more recently, in philosophy, Zalta (1988; 1993) defines abstract objects (read "types") as encoding properties, while ordinary objects (read "objects") as exemplifying properties. Zalta's theory defines as many abstract objects as there are combinations (power sets) of properties. Thus, there are no two abstract objects (types) with exactly the same properties (exists! x(A!x & forall F(xF=q)) 1, where q has no free xs), but two ordinary objects (objects) with exactly the same properties may be distinct. The set of all abstract objects (types) and the set of all ordinary objects (objects) cover the universe (forall x(O!x v A!x)) and do not intersect (not exists x(O!x & A!x).
Cardelli and Wegner (1985) view types as sets of values in their typed lambda calculus language fun. Cardelli and Mitchell (1994) define objects and classes this in way:
Object-oriented programming is based on record structures (called objects) intended as named collections of values (attributes) and functions (methods). Collections of objects form classes. A subclass relation is defined on classes with the intention that methods work 'appropriately' on all members belonging to the subclasses of a given class. (p. 295)In object oriented programming, Booch (1994) defines type, object and class:
Typing is the enforcement of the class of an object, such that objects of different types may not be interchanged, or at the most, they may be interchanged only in very restricted ways. (p. 66)A class is a set of objects that share a common structure and a common behavior. (p.103)
An object has state, behavior, and identity; the structure and behavior of similar objects are defined in their common class; the terms instance and object are interchangeable. (p. 83)
Hailpern and Nguyen (1987) list several meanings for objects and classes: object is merely a new name for abstract data type (ADT); objects and classes are a concrete form of type theory; objects and classes are a way of organizing and sharing code.
Although these definitions are different, there is some common thread throughout. Wegner (1988) sorts it out by subdividing the subject into four separate perspectives: classification, inheritance, mathematical, and philosophical:
Formalisms may infer the type of an expression either by determining the denotation and then determining the type of the denotation, or by inferring the type in the typed lambda calculus. These two methods do not necessarily arrive at the same conclusion (see Figure 8).
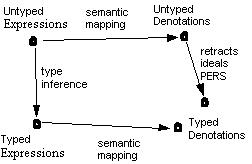
Classification in logic and computing can be by inference and unification, or by abstraction and specification. Classification in programming languages is one of three paradigms: state transition (statements), communication (objects), and classification (classes). Classification is complicated by polymorphism in its various forms.
The inheritance perspective is of particular importance in this thesis. Cook, Hill, and Canning (1994) distinguish between inheritance and subtyping and identify three types of inheritance: object inheritance (similar to C++'s inheritance), class inheritance (similar to Smalltalk's metaclasses), and type inheritance. But Cook's "object inheritance" is quite different from the inheritance in Wegner's object-based languages with inheritance. This alternate model of inheritance is called delegation and is important to this thesis in the Chapter 4. Delegation replaces the concept of a class with a prototype (Lieberman 1986). Any object can act as a prototype. When an object receives a message for which it does not have a method, it delegates responsibility to its prototype. Multiple inheritance in delegate languages is made possible by maintaining a list of prototypes for each object. Lieberman shows that delegation is more powerful than inheritance by showing that delegation implements the functionality of inheritance, but inheritance does not implement all the functionality of delegation.
It should be clear that there are no clear and absolute definitions of, or distinctions between, the terms type, class, and object. Class may not even be considered a primitive definition at all, as classes may be derived from objects (Abadi & Cardelli 1996). It all depends on one's perspective. It is clear, however, that types provide intentional definitions for objects and that objects represent instances (that may exist in some real or hypothetical world) which may be categorized according to type. The definition of class is far less clear: according to the programming language, class is the same as type (as in C++), or class is just an vehicle for ad-hoc inheritance and has nothing to do with type (Wegner 1988) (as in Java). Some new languages do not even use classes, but use prototypes instead and are still well-typed (Abadi & Cardelli 1996).
Object oriented programming languages are represented by both paradigm-specific languages (Simula (Birtwistle et al. 1979), Beta ( Kristensen, Madsen & Moller-Pdersen 1988), Smalltalk (Goldberg 1983)) and languages that have evolved from languages in other programming paradigms (C++ (Stroustrup 1991), Modula-2 (Wirth 1988)). Object-oriented is an over-applied term; many "object-oriented" languages fail to provide all the properties (objects, classes and inheritance) generally agreed upon as minimally defining "object-orientedness". Wegner (1988) provides a classification of near-object-oriented languages:
| objects | = | object-based | (Ada,Actors) |
| + classes | = | class-based | (Clu) |
| + class inheritance | = | object-oriented | (Simula, Smalltalk, C++) |
Abadi and Cardelli (1996) take a very wide view in their analysis and formalization of object oriented languages, encompassing typed and untyped languages, class-based and object-based languages, and embedding and delegation languages. They start off with a simple, untyped, non-inheriting record calculus. Objects are considered primitive and consist of a collection of methods (fields are modeled as just methods with no parameters - which implies that the language has method updates). From this simple calculus, they show how classes and inheritance can be modeled in terms of objects. Thus, they show clearly that objects can be taken as the primitive of object oriented programming.
Abadi and Cardelli model almost all the object oriented programming languages using their simple object calculi. Object oriented languages may be divided into class-based languages and object-based languages. In this model (unlike Wegner's), inheritance can occur in object-based languages. In class-based languages, classes act as templates for instantiating objects; in object-based languages, prototypes (concrete and fully functional objects) take the role of classes, and objects may be instantiated from them by cloning.
The inheritance roles in object-based languages are termed the donor (the "parent") and the host (the "child"). Object-based languages may be divided according to how they incorporate attributes of the donor object into the host object - either implicitly or explicitly, or, orthogonally, embedded or delegated. Implicit inheritance incorporates all attributes of the donor into the host, while explicit inheritance incorporates only specified attributes (but some languages may allow inheritance of groups of attributes, which implies that implicit/explicit inheritance is a continuum, not a bipolar quality). In embedded inheritance the donor attributes are copied into the host (although optimizations may blur this model); in delegate inheritance the donor attributes remain with the donor and the host accesses them as needed via a reference. Multiple inheritance is easily implemented by having each object maintain a list of donors.
Classes can be modeled on top of object-based languages merely by making host objects non-concrete, and differentiating the inheritance relationship between isa and instance-of for sub-classing and object instantiation respectively. Furthermore, interfaces (as per Objective-C and Java (Arnold & Gosling 1996)) are easily modeled as class-objects whose attributes include only method descriptions and no fields.
Abadi and Cardelli (1996) also make a contribution by clearly elucidating the constraints on method overriding and fields (attributes) in subtypes. It is a consequence of subsumption ((a:A AB) a:B) that method arguments are contravariant and return types are covariant. That is, any method that overrides a method of a parent type may generalize (but not specialize) the arguments and specialize (but not generalize) the return type. Furthermore, it is also a consequence of subsumption that record (or object) fields are always invariant. That is, a subtype may not change the type (generalize or specialize) of a supertype's field that may be publicly updated. In spite of this, some languages (for example, Eiffel (Meyer 1992) and Beta (Kristensen et al. 1988)) still allow covariance in method argument types. Beta uses run-time checks to catch errors resulting from covariant arguments.
Although many concept mapping languages are not programming languages per se, their typing can be understood with reference to the object oriented paradigm.
Concept maps are graphs, in the general graph theory sense, where nodes and arcs may be labeled and annotated with a type. Furthermore, if one does not make the restriction that arcs must be binary, but allows arcs to have arbitrary arity, then concept maps are hypergraphs. Hypergraphs are just graphs where the arcs can terminate on any number of nodes (Drewes & Kreowski 1990). A graph (in the graph theory sense) is just a specialization of a hypergraph where every arc (or edge) is binary (has an arity of 2).
If concept maps are to be modeled using either Crimi's relational grammars or Wang and Lee's semantic interpretations, then the obvious choice is to allow concept maps to be hypergraphs, since neither Crimi's nor Wang and Lee's formalisms assume binary relations (see Section 2.1.2). Furthermore, generality alone argues for a hypergraph interpretation. There is also the compelling argument that some situations are difficult to model without non-binary relations, for example, between (Sowa 1984):
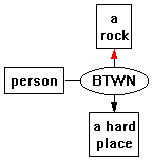
Here, BTWN is just the label on a trinary arc. It can be argued that non-binary arcs can be replaced by nodes with special restrictions (for example, the trinary between arc in the preceding example could be replaced by a node which is restricted to have one incoming and two outgoing arcs). But such a model can often lead to complex semantic restrictions. The more general, hypergraph, interpretation is taken as the superior because such a concept mapping system can subsume both between models.
If one models general concept maps as hypergraphs, it becomes easy to map between concept maps and relational structures just as Crimi maps between general visual language and relations to apply relational grammars, and Courcelle (1990) maps between hypergraphs and relational structures. Corrandini et al (1994) show how labeled graph grammars can be used to specify entity-relationship diagrams where the type of the arcs (relations) restricts the node (entity) types on which the arcs may terminate. Thus, the definition graph,
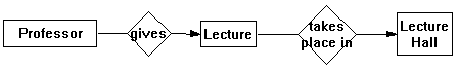
will restrict an arc (relation) of type gives to connecting only a node (entity) of type Professor to one of type Lecture, and will restrict an arc (relation) of type takes place in to connecting only a node (entity) of type Lecture to one of type Lecture Hall. Corrandini et al work only with graphs (and not hypergraphs), but the principle projects to hypergraphs in a straightforward manner. As a case in point, Crimi's relational grammar for visual syntax is very similar, but works with hypergraphs (see Section 2.1.2).
Both Corrandini et al and Crimi's work is applied to labeled (hyper)graphs. But it is a simple matter to extend this work to deal with typed hypergraphs. Here, labeled hypergraph is taken to be a special kind of typed hypergraph where the types of nodes and arcs are taken from a flat type lattice: there in no subtype/supertype relationship between the different types (other than the universal and absurd types). In contrast, in a typed hypergraph the types of nodes and arcs are taken from an arbitrary type lattice: there exists a subtype/supertype relationship between the different types (see Figure 9).
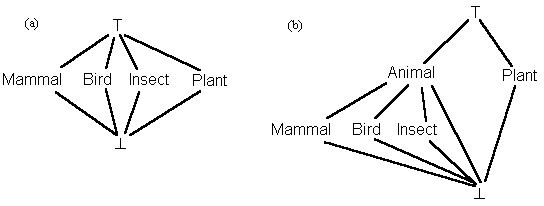
Typed hypergraphs make Corrandini's arc constraints slightly more complex because subsumption must be taken into account. Take, for example, the following definition graph under the typing of Figure 9 (b):
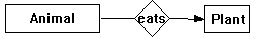
In a flat-typed (labeled) world, this definition allows an object of type animal to eat a plant:
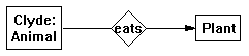
but it wouldn't allow a more specific (specialized) animal to eat the same plant:

because Mammal isn't the same label as Animal. Clearly, knowing more about Clyde's type shouldn't necessarily bar him from eating. In a typed hypergraph world Clyde can eat: Informally, the type of the node at an arc terminal is legal if and only if it is some subtype of the type of the node at the corresponding terminal in the arc's definition. In other words, it's legal to put a Mammal node at the start of an eats arc because Animal subsumes Mammal.
But there can be a type lattice for arcs as well as nodes (for example, eats may be a subtype of consumes, which may be a subtype of effects). Therefore, the reference to an arc's "definition" in the previous paragraph needs to be replaced with a reference to an arc's "supertype": The type of the node at an arc terminal is legal if and only if it is some subtype of the type of the node at the corresponding terminal in all of the arc's supertypes.
In more formal terms, one needs to discuss instances and types separately. If one is discussing instances, the arcs can terminate on subtypes of the definition-allowed nodes due to subsumption (e.g. (Mammal <: Animal Clyde:Mammal) Clyde:Animal). If one is discussing types, arcs are covariant in the node types that they may terminate on. This is easy to see by noticing that the type of an arc may be considered to be the product of the types of the nodes on which it can legally terminate. For example, if binary arcs of type A are restricted to terminate on nodes of types X and Y, then A =def X Y. Abadi and Cardelli (1996) offer a proof that product types are covariant:
A pair <a,b> with left component a of type A and right component b of type B, has type AB. If A <: A' and B <: B', then by subsumption we have a:A' and b:B' , so that <a,b> has also type A'B'. Therefore any pair of type AB has also type A'B' whenever A<:B' and B<:B'. In other words, the inclusion AB <: A'B' between product types is valid whenever A<:A' and B<:B'. (p. 20)Since arc types are product types, and product types are covariant, then arc types are covariant on their "arguments" (the types of the nodes on which they may legally terminate).
Thus, the relational grammar approach of Crimi, and
the labeled graph grammar approach of Corrandini et al can be
applied to typed hypergraphs (and concept maps in particular)
with only a small addition to account for subsumption and covariance.
Software formal specification has spread from the academic environment to industry. Craigen, Gerhart, and Ralston have conducted detailed studies of twelve large industrial software development projects in commercial, exploratory, and regulatory domains (Craigen, Gerhart & Ralston 1993; Gerhart, Craigen & Ralston 1994). They concluded that, though formal methods are still not mature, they "are beginning to be used seriously and successfully by industry to design and develop computer systems" (p. ii). Formal methods are being applied to large-scale projects, and are used primarily for system assurance, domain analysis, stakeholder communication, evidence of best practice, re-engineering, and system certification. While tool support was found to be lacking, Craigen, Gerhart, and Ralston (1993) found tool support to be "neither necessary nor sufficient for successful application of formal methods" (p. 70); but rather, successful application depends on local skills, sustained guidance by an expert, management support, and technological change providing an impetus for adoption of formal methods.
Many of Craigen, Gerhart, and Ralston's case studies used Z or Z-derived methods as the formal specification notation. Z is a relatively simple algebraic notation based on set theory which makes heavy use of schemata to block structure the specification. Z has been used to model a wide range of applications. Hayes' (1987) book contains case studies of Z specifications of the UNIX file system, telephone networks, data dictionaries, assembler languages, user name authentication, time services, reservation services, and various parts of the CICS operating system. Craig (1991) describes an extended Z specification of the blackboard architecture commonly used in AI applications, as well as the related CASSANDRA architecture. Halasz and Schwartz (1990) use Z to specify a hypertext architecture, which has been extensively adopted and extended (Gronbaek et al. 1994; Gronbaek & Trigg 1994; Hardman, Bulterman & Rossum 1994).
One of the attractive features of Z is its compatibility with the object-oriented paradigm (Craig 1991). Classes in object-oriented programming languages are based on block structure records (Madsen 1988) which maps directly onto Z's schemata. Classes form the types of object oriented programming languages, and objects are instantiated from classes - just as schemata form the types of Z and variables are instantiated from schemata. Furthermore, class inheritance is considered fundamental to object-oriented programming and design (Pree 1995; Kristensen, Madsen, Moller-Pedersen & Nygaard 1988; Snyder 1988; Wegner 1988) and is partially modeled in Z: schemata may be included in other schemata. This simple inclusion scheme allows Z to model both single and multiple inheritance. (In addition, schemata may be combined by various operators such as conjunction, disjunction, and sequential composition; this powerful tool has no mapping in the object-oriented paradigm.)
This chapter has dealt with the object oriented paradigm and its relevance to concept maps. It also briefly introduced specification and the Z specification language.
Pivotal to the object oriented paradigm are the notions of type, class, and object. Unfortunately, there are no clear definitions or sharp distinctions between these terms. Types intentionally describe objects, which are more-or-less concrete instances. But the definition of class is more complex, sometimes being taken as the same as type, sometimes being taken as just an implementation vehicle. Both the notion of types and classes is clouded by the notion of meta-types and meta-classes.
Several relevant issues in object oriented languages are discussed. These will be of importance in chapter 4. There are many classifications of object oriented languages: typed vs. untyped, type inheritance vs. code-sharing inheritance, class-inheritance vs. prototyping, and dynamic vs. static typing to name just a few. Of particular interest is class-inheritance vs. prototyping: prototyping blurs the distinction between type (or class) and object because a fully-functional object can act as a "type" or class when an instance is cloned from it. Prototype languages with no classes may also use inheritance in two ways: by embedding (copying attributes) and delegation (reference to the original donor).
Concept maps can be modeled as hypergraphs, where the arcs need not be binary, but may be of arbitrary arity. In this model, concept map arcs can be mapped onto relations and can be dealt with using the semantics of relational grammars (Courcelle 1990) and hypergraph grammars ( Corrandini et al. 1994). Using these grammars, arcs can be easily constrained as to the type of the nodes their terminals may be anchored to. This work all deals with "flat" type lattices for node and arc types, but it is easily extended to an arbitrary type lattice model by using subsumption and Abadi and Cardelli's work on covariance in object oriented language theory.
The role of specification is also briefly outlined. Specification and specification tools have moved from academia to industry. Z is a popular and simple specification language based on set theory. A dialect of Z is used to specify Constraint Graphs in chapter 5.
 Chapter 2
Chapter 2
 index
index
 Chapter 4
Chapter 4
 Constraint Graphs: A Concept Map Meta-Language (PhD Dissertation), Department of Computer Science
Constraint Graphs: A Concept Map Meta-Language (PhD Dissertation), Department of Computer Science