
Concept mapping techniques, both formal and informal, are useful in knowledge representation, decision support, education, documentation, meeting support, brainstorming, and a host of other areas. Computer support of concept mapping is essential since creation and revision of hand-drawn maps is far too labor-intensive. Computer support of concept mapping also holds the potential benefit of additional services such as automatic inconsistency detection, incompleteness detection, suggestion of potential extensions, and the use of various elicitation techniques. However, a dichotomy exists between the human user's need to work with a flexible and forgiving (hence informal) system, and the computer's need for a (formal) system with strong semantics. The full benefit of computer supported concept mapping will not be reached until the dichotomy is bridged. This paper suggests a few avenues for research in this area.
Concept maps are an intuitive visual knowledge representation technique. They appear to have more "computational efficiency*"10 than some other forms of knowledge presentation such as pure text or predicate logic12.
Concept maps are graphs consisting of nodes with connecting arcs, representing relationships between nodes10. The nodes are labeled with descriptive text, representing the "concept", and the arcs are labeled (sometimes only implicitly) with a relationship type.
Concept maps can represent knowledge on the very formal level,
as in Gaines' KRS system, where concept map structures act as
a complete interface to a knowledge representation language7 based
on Classic2. Another formal concept mapping system is the GrIT5
system which edits conceptual graphs* and processes
them using PEIRCE6. But concept maps can also represent knowledge
on a much less formal level if the system puts fewer constraints
on the graphical "syntax"† . Concept
maps tend to be much easier for human users to understand than
other knowledge representations such as predicate logic12‡.
These two factors, intuitive understanding and both formal and
informal knowledge representation, are of great importance: Both
novices and experts can potentially use the same media, novices
being free to express themselves informally and without constraint,
while experts can express themselves under the constraints of
very formal semantics which allows for computational support.
Section 2 and 3 describe formal and informal uses of concept maps, respectively. Section 4 describes concept map generation (editing) and requirements for computer-supported concept map editing. Section 5 describes the conflict between formality and informality that arises from the requirements. Finally, section 6 deals with some of the possible solutions to the problem.

Concept maps are not computational unless they have an associated semantics. That is, the maps' node and link types and their interconnections must be constrained to allow for computer support. Indeed, computational concept maps form the primary representation system for many works including language analysis17, Ausubel's assimilation theory3 for human learning; Leishman's analogical tool11 for reasoning about situations based on analogy with previous cases, influence diagrams3 for decision support and expert system development, and Gaines' KSSn/KDraw tool7 for knowledge representation in expert systems. All of these constrain the maps to very specific, if not explicit, types on nodes and arcs.
For example, Gaines' KSSn/KDraw tool allows the user to draw concept maps using a direct manipulation graphical interface similar to the MacDraw program. Extensions include arcs who's endpoints move with the node objects and context-specific popup menus. All nodes are labeled and visually typed based on graphic surround (see figure 1). For example, concept types have elliptical surrounds and individual types have rectangular surrounds. The node types correspond directly to the features in Classic: primitive concept, concept, individual, constraint, role, and rule. Arcs are unlabeled and only incompletely visually distinguished. For example, is-a, constrained-by, and value type arcs are all represented as uni-directional arrows, while the mutually-exclusive type is represented by a simple line. The incomplete visual distinction of arcs does not mean they are not strictly typed -- arc types are always unambiguously specified by the types of their terminal nodes. The interface disallows any graphical structure that does not make semantic sense.

KDraw's concept maps are computational in the same way as Classic2 is computational as a knowledge representation and inference language: The class (or type) of an individual can be inferred by the attributes of the individual and those of the concepts, and rules may be fired based on the inferred class of an individual.
Another example of a formal concept mapping system is the GrIT system which graphically manipulates conceptual graphs17 and interfaces to the PEIRCE system in much the same way as KDraw interfaces to the Classic compiler.
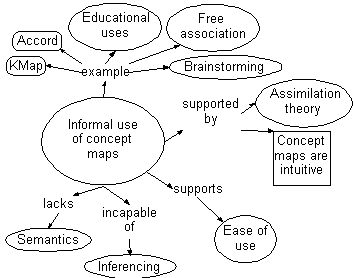
Concept maps without formal, computational semantics are not without utility. Although they are not computational from a computer's point of view, for a human they appear to have greater "computational efficiency" than other forms of knowledge representation, such as text10. Informal concept maps have long been used in education both to present concepts and as a vehicle for determining student understanding13,10. Informal concept maps are usefully applied to knowledge engineering for brainstorming and free association techniques17 where "completeness is more important than neatness and rigor" (p. 299).
Accord9, a program which allows users to draw concept maps with a graphical direct-manipulation interface similar to that of KMap but without semantics, has been applied to brainstorming, planning, knowledge elicitation, documentation, presentation, decision support, and meeting facilitation in such diverse areas as research planning, computer networking, marketing, education, oil and gas strategy planning, computer program design, formal language design, academic paper planning, literature analysis, and personnel planning. The author's experience to date has been that most people enthusiastically adapt to reading and understanding informal concept maps (which concurs with Lambiotte10) and readily learn to create and modify concept maps. The author has introduced computer-supported concept mapping to individuals who could then independently draw concept maps within five minutes, and to groups using separate workstations with a shared concept map workspace who where collaborating on their topic area within fifteen minutes.
In spite of the many virtues of concept mapping, and its use in specialized fields such as education, it is not ubiquitous. This section explains why, and offers an informal requirements specification for computer-supported concept map editors: ease of use, and various potential services.

The claim has already been made that concept maps are intuitively easy for people to understand and manipulate. One would therefore conclude that concept maps should be common representational media today. But this not the case (at least not outside of specialized circles.) The reason for this apparent contradiction is that, before the recent age of powerful graphical workstations, concept maps were difficult and time consuming to produce. Concept maps had to be carefully preplanned to avoid excessive erasures or recopying when large swaths of the map had to moved to make room for an unanticipated insertion. Even worse, revisions or extensions to concept maps were usually just as difficult to produce as the original because it usually involved recopying the entire map. Compounding the problem was the fact that large concept maps need to be broken up into a web of composite concept maps, and navigation among these inherently non-linear references was difficult and awkward when imposed on linear media such as books. These problems kept concept mapping techniques confined to static media such as printed media and specialized purposes such as student modeling in education and language analysis. Even these applications had to confine themselves to relatively small conceptual structures.
That was before the introduction of cheap and easily accessible computers with full color graphical interfaces. Graphical workstations remove the labor-intensive task of concept map design. Graphical concept map editing programs such as KDraw, KMap, and Accord allow users to quickly slap down ideas (nodes and arcs) onto the workspace without having to carefully pre-plan the layout. These editors allow authors to easily slide concept map nodes (or groups of nodes) around the workspace: the editor takes care of maintaining relationships (arcs) among the nodes. These and other features, allow for easy creation, modification, and copying of concept maps by non-experts. Computer workstations can also be used as a display media for concept maps. This affords easy navigation between related concept maps and other media; user annotation and extension; and user feedback to the author.
Having made the claim that graphical workstations and concept map editors are essential to the use of concept maps, one must ask what the requirements of a concept map editor are.

The first thing one must consider, when trying to establish requirements for anything, is who are the users? In the case of a concept map editor, the users will be almost anybody -- from young children to engineers, managers, teachers, and scientists. Most of the users are not going to be particularly skilled in the use and manipulation of computerized concept maps; nor are they likely to be willing to invest much time learning how to use concept maps. Besides the obvious -- that a concept mapping editor must have a very good, intuitive user interface -- the fact that the users are not concept map experts dictates that the editor cannot enforce formality on the authored concept maps. Untrained users cannot be expected to conform to the constraints of a formal semantics, for they will be frustrated and distracted if they must change their thinking to conform to the structures of a formal system. But rather, the users must be allowed to concentrate on the task at hand in an unrestrictive environment. This is not to say that concept map editor cannot support formality (and the services that can come with formality), just that it must not force formality on the users.
Not only do individual users create and edit concept maps, but groups of users, together, also create and edit concept maps. Since groups are composed of individuals, the arguments for support of informal concept maps for individuals also applies to groups. But groups have an even stronger need to avoid being forced into formal concept mapping (at least at the early stages). Synchronous groups (those meeting all at the same time, whether at the same place or remotely) are usually pressed for time, and cannot afford the luxury of spending time hesitating over the syntax of a formal system17. For example, the author has acted as a scribe creating concept maps on a large, shared computer screen during group brainstorming, and can verify the fact that speed, rather than semantic precision is required. Furthermore, in group sessions with shared input into the workspace, individuals who are not quite as adept at using the system tend to hesitate to contribute for fear of showing their "incompetence" on the system. Formal systems greatly accentuate this "free riding" problem14.

Having established the need for support of informal concept maps, this section enumerates a few of the services that concept map editors may offer the user. Several of the basic editing services have already been described, and these do not differ greatly from those of good, object-oriented graphics editors, other than specific support for arcs being anchored to nodes. These services will not be discussed further here (see "A Concept Map Based Approach to the Shared Workspace."9 for further discussion on some of these points).
A concept map editor might be able to offer inconsistency detection. Formal concept map systems can insure the formal, syntactic integrity of the map is maintained. Gaines' KDraw does this by simply not allowing the user to make "non-syntactic" constructs. For example, the system will not draw an arrow arc from a rule node to a constraint node because such a relation is not syntactically legal.

But inconsistency detection can go a step further than syntactic integrity to address semantic integrity. For example, in a gIBIS4 concept map (see figure 2), an argument node may have a supports link to a position node. If a user then attempts to draw an objects-to link from the same argument node to the position node, an editor could either refuse the operation or somehow flag the structure as inconsistent. Note that gIBIS syntax allows both types of arcs in this situation, but it is a semantic violation to have both arcs between two nodes. This simple example addresses only shallow semantics: one can envision deeper semantic inconsistency detection when an argument node does not logically apply to the position node it is linked to. This level of semantics usually involves some degree of natural language understanding or other technology (such as theorem proving), and will not be discussed in this paper.
Supporting incompleteness detection is usually more complex than inconsistency detection. An example of incompleteness is a gIBIS position node that lacks both supports and objects-to links. Note that during editing, all concept maps necessarily contain incomplete constructs. An editor must devise some means by which it can inform users of incompleteness at appropriate times, and not deliver "annoyance" messages during editing.
A concept map editor may not be able to detect valid incompleteness because it may not have information about the complete system. For example, KDraw could claim a lowest-level concept node as incomplete because it has no associated rule node (the reasoning being that if an individual is classified under this concept, something must be missing because nothing will happen). But this assertion would not be valid, as the concept map may be later composed with other concept maps (which may make the concept more useful) or it may be used by other systems, such as HyperCard, which may make use of the classification. KDraw does not attempt to detect this type of incompleteness for these reasons.
Users of a concept map editing system can be prompted by the system to build the map. To use the gIBIS example again, a novice user may start out with a map containing only a single issue. The system could prompt the user by asking if he/she has a position on the issue (indicating a responds-to link between a new position node and the issue. Having entered a new position, the user may be prompted for arguments supporting or objecting to the position. Such a line of questioning could guide a user through a complete construction of a gIBIS map.
Prompting can be more subtle than this however. For example, if an incompleteness is detected, the user may be prompted to fill in the relevant part of the concept map.
Prompting may not be tied directly to the shallow* type structure of the concept map, as it is in the previous example. For example, prompting may be based on the deep semantics of the concept map: a system like KDraw could prompt users to fill in values for roles that an individual is inferred to possess.
A concept map editor may act as an intelligent agent participant in the construction or criticism of a developing concept map. For example, in a gIBIS map, the editor may notice that a particular argument node could support a particular position node. The editor itself could tentatively draw in the supports arc between two nodes, prompting the user for confirmation.
Besides the prompting already mentioned, there exist other direct elicitation techniques for the extension of concept maps. For example, laddering8,3, is a technique that applies to concept hierarchies. The technique asks why questions to solicit superconcepts (concepts higher in the hierarchy) and how questions to solicit subconcepts (concepts lower in the hierarchy).
Inferencing in formal concept maps has already been discussed. KSSn/KDraw acts as a complete expert system shell. But there are other forms of inferencing that can be applied to concept maps. For example, several decision support systems make use of various hierarchies that can be interpreted as concept maps. One can view gIBIS as such as system. A gIBIS map could be made computational by allowing multiple users to annotate the position nodes related to a particular issue, with their votes. The position adopted for the issue would be the one with the highest number of votes.
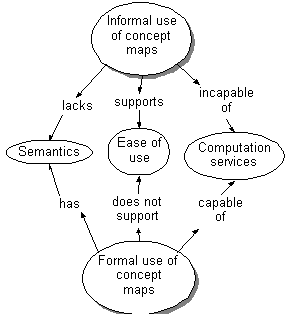
The major requirements of a concept map editor include handling informal concept maps and offering various potential computational services. But these two requirements are in direct opposition, for the computation services (inconsistency detection, incompleteness detection, prompting, extension suggestions, elicitation, and inferencing) all require formal concept maps. There is a dichotomy between the need for informal and formal concept maps. Fortunately, there are two points that alleviate this quandary: A system can concurrently support both informal and formal concept maps, and formality/informality is a continuum, not a dipole.
Concept mapping systems display a range of formality. On the extreme informal end is KMap, which allows the user complete freedom in drawing a map. Slightly more formal is Accord, which enforces arc labels in a distinct style from nodes. Accord also restricts arcs to being between nodes (and not between other arcs). Toward the formal end of the spectrum is KDraw, which imposes a strict set of types on all nodes and arcs (arc types are strict but implicit), however no attention is paid to the semantic content of the nodes. Even more formal are analysis systems and tools such as Leishman's analogical tool and the GrIT conceptual graph editor5 which not only type nodes and arcs, but also pay attention to the semantics of the contents. (See figure 3.)

The requirements dictate that a concept mapping system must support informality, but this does not mean that it cannot also support formality at the same time. There is no inherent reason why a system cannot do whatever processing it can on the parts of a map that conform to its syntax and semantics while ignoring the parts of the map that it finds unintelligible.

This section considers a few lines of attack on the formality/informality problem. The problem is considered in the context of current feasible technology; that is, semantics of node and link types are considered and not the semantics of their contents. It is assumed that labels on nodes and links are in natural language* and the current level of natural language understanding does not allow for practical use of semantics here.
The approaches discussed in this section fall into three broad (and inter-related) categories:
semi-formal semantics (section 6.1.), which offers a way out of having to understand the deep semantics of the content (natural language) of concept map node and link labels,
type inference (section 6.2.), which may allow the program to infer the type of concept map nodes and links when the user has not specified them,
type theories (section 6.3.), which may be either pre-specified or user specifiable/extendible and offer a reasonable means for the user to take on responsibility for object typing.
Note that neither semi-formal semantics nor type inference offer an operational approach to the problem as both assume the existence of a type theory. It is only the third approach, type theories, which is operational enough to form the basis of a workable system. The other two approaches, particularly semi-formal semantics, are none-the-less a necessary part of a workable system.
An approach taken by Smolensky, Bell, Fox, King, and Lewis in the EUCLID/ARL system16 is semi-formal semantics. EUCLID is a hypertext environment intended to support reasoned argument via information layout that clarifies argument form. Their aim is not to replace human reasoning, but "to give users the expressive and analytic power necessary to elevate the effectiveness of their own reasoned argumentation" (p. 217). They divide reasoning into two levels: above "the Divide" is domain specific assertions such as "Lower interest rates lead to bull markets", and below are assertions like:
Claim C1 supports claim C2.
Claim C is the main point of argument A.
Claim C is made by author S.
Claim C made by author S1 contradicts claim C2 made by author S2.
Term T is used by author S1 to mean phrase D1 but by author S2 to mean phrase D2. (p. 218)

One could describe "the Divide" as separating the shallow semantics (the semantics of the object types -- below "the Divide") and deep semantics (the semantics of the content of the objects -- above "the Divide"). EUCLID deals only with shallow semantics (below "the Divide") and this allows EUCLID to understand enough of an argument to generate information layout based on the argument form. Note, however, that EUCLID cannot understand the deep semantics of the argument, so cannot detect many deep inconsistencies, irrelevancies, or other errors. That is, EUCLID could detect that some argument both supports and refutes a certain claim, but it could not detect that "the sky is blue" is not a logical consequence of "bull markets".
In translating the ARL examples above (the bulleted list) to a concept map, claim, argument, author, term, and phrase would be considered node types in a concept map, while support, main-point, made-by, contradicts, used-by, and means would be considered link types (see figure 4).
The division between shallow and deep semantics is also the division between what is and is not feasible with current technology. Thus, semi-formal semantics is an important concept in the design of any concept mapping system that ranges over formal concept mapping. It is not operational, however, because it assumes the existence of a type theory.

Another obvious angle of attack on the formality/informality problem is to establish a formal semantics for set of types (a type theory) and infer the types of nodes and links that users do not specify† . On the surface, it would appear that this would require advanced natural language understanding, but this may not necessarily be the case.
It may, for example, be possible to do analogical structural matching11 between the target map and a library of example typed maps to infer missing types in the target map. The example library could be composed of carefully constructed "typical" examples, perhaps very specific to the domain; or examples may simply be past, completed concept maps.
Another approach is that the system may look for keywords in the node and link content to obtain hints at the types (without necessarily understanding the content). Keyword dictionaries would have to be domain-specific (or even user-specific15) to account for large differences in word usage between domains (and people).

The problem of type inference could be skirted: The system does not necessarily have to assume all of the burden of attaching type information to nodes and links. As long as the task is made easy and intuitive, the burden can be shifted to the user. Part of the problem users encounter when using a typed system such as gIBIS is that they have difficulty classifying objects from their discourse domain into the limited set of types offered by the system. Merely offering them a set of synonym type names may be enough to significantly mitigate the problem, particularly if the synonyms use the vocabulary of the discourse domain.
For example, a group of application program designers may use module as a synonym for gIBIS's issue and responsibility as a synonym for position In this way, when the users are contemplating the issue of the functionality of a program module, they can draw it as a module node then relate this (responds-to) to a responsibility that the module could potentially take on; argument nodes relate to the responsibility through supports or objects-to links. The users would then be visually discussing the problem using a domain-specific (and therefore user-comfortable) vocabulary, while the system can operationalize, and offer services, based on the gIBIS model.

While simple synonyms may be a helpful tool, building up a type hierarchy for nodes and links offers more power and flexibility. This is particularly true for systems that may offer services through several different agents, which may have varying levels of knowledge about the types. In a type hierarchy, the above program module example would include "module is-a issue" and "responsibility is-a position" (see figure 5). This way, an agent that knows only about the gIBIS model could deal with module and responsibility by virtue of them being issues and positions, respectively. This agent, for example, might be able to answer certain questions by enumerating the positions (responsibilities) pertaining to an issue (module). An agent that has more knowledge about module and responsibility types could deal with them directly, applying whatever specialized processing is necessary. This agent might be able to accomplish more domain-specific tasks such as building the outline for a formal specification of a program from the concept map (based on linked responsibilities and modules). Both these kinds of agents can work on the same data because an agent encountering an object of an unknown type need only trace up the type hierarchy tree until it encounters a type it does know about, and then deal with the object as if it were the known type.
Such a type hierarchy subsumes the previous "synonyms" model, since the synonyms behavior can be reproduced by merely hanging new types (that no agent knows of) off nodes in the type hierarchy tree. The only restrictions are that some operational type should appear on every path up the tree. (This implies that the root is an operational type.)
Type hierarchies are quite domain-specific due to conflicts in vocabulary between domains. There is no universal type theory. For instance, the type class means two different things depending on whether the context is a programming domain (class = object-definition) or an education domain (class = group-of-students). Thus, a concept mapping system that takes advantage of type hierarchies would have to contain libraries of type hierarchies, one for each domain in which it was used. This leads to another problem: a concept map editor will likely be used for some purpose that its creators had not anticipated. No one can develop type hierarchies for all possible domains.
The only way to accommodate unanticipated domains is to allow the users to extend type hierarchies themselves. That is, given a basic, operational type hierarchy, users should be able to edit it to add their own type names as appropriate. Another argument in favor of user extensible type hierarchies is terminological differences between people, even within the same domain. Shaw has observed significant differences between domain experts in the way they use terms15.

There are several problems to be overcome when allowing user type extendibility. One problem is how to allow users to edit type hierarchies in a simple and intuitive manner*.
Another problem is, if users are to be allowed to make up types as they go along (as they will), they will not be disposed to interrupt their current task to go off and edit a type hierarchy; but rather, it is more appropriate to let them merely enter the new type into the concept map and deal with the details later. One simple way the system can deal with this is to enter new types into the hierarchy just under T. In this system, T is the root (top) of the type hierarchy from which all types inherit. If a type interpretation ever defaults to T it is interpreted as "undefined". Thus, when users enter new type names in the heat of discussion, the types will simply be accepted, but later the users can edit the type hierarchy, moving the new types from under T to some appropriate place in the hierarchy.
Another wrinkle one must deal with when allowing user defined types is whether to allow the user to endow the new types with semantics. If one allows user-extensible semantics, a whole world of possibilities and corresponding problems is unleashed. One can envision user-assigned type scripts, relational properties, attributes, etc., but these will not be discussed in this paper.
User extensible types can be very powerful, but type definition is probably beyond the capacity of a large segment of the potential user population. A judicious set of domain-specific type models each of which can be copied and adapted is probably most appropriate.
All this flexibility must be housed inside a concept map editor that does not impose constraints on drawing. But the tool should be able to offer services (which require formality) and so must be able to both understand and extend type theories. Of course, these services are only available to users if they are choose to convert the graph, in whole or in part, to conform with the type system.
There already exist excellent examples of editors which handle formal concept maps. KDraw (part of KRS) is a formal concept map editor which constrains the concept maps to a visual form of the Classic knowledge representation language. KDraw can export the information contained in the map for processing by a Classic engine. GrIT5 is a concept map editor which handles conceptual graphs. The conceptual graph graphical constructs are interpreted into linear format for processing by PEIRCE6.
At the other end of the spectrum are informal concept map editors such as KMap (another part of KRS) and Accord. While these have no formal semantics, and so cannot offer the many services which require formality, they still have a great deal of value for their human-readable and easily editable concept maps.

The requirements specified in this paper call for a union or merging of the formal concept map editors and the informal ones. In fact, both Kmap and Accord start to fulfill this role. KMap can be used to export to the Classic compiler, and the compiler will only take notice of the Classic object types that it knows about.
Accord is the first stage of a research project aimed at supporting both informal and formal concept mapping. Accord has been designed as a very modular concept map editor which acts as an almost semantics-free base on which formal constraints can be layered. By itself, Accord is a simple, graphical concept map editor, allowing users to manipulate nodes and arcs between the nodes. The nodes and arcs all have associated user-specified type names. Additionally, nodes are named by the user, and this name is displayed inside the node. Most of the figures in this paper were generated using Accord.
Accord is designed to accommodate additional layers which add semantics to the graph editing. One can also associate user-extendible type theories with accord databases. Accord itself interprets types in terms of visual attributes (such as surround shape, fill color, border color and text color) of the corresponding objects, but semantic layers may interpret types in more meaningful ways.
Layers on top of Accord could either offer services directly or could take the approach of KDraw and GrIT and export processing to external facilities such as Classic and PEIRCE. As mentioned in the previous section, Accord layered services would have to account for the informality of the system, searching up the type hierarchy to attempt to coerce unknown types to known types before processing. For example, with an appropriate layer, Accord could closely imitate KDraw and support Classic knowledge processing. The difference being that Accord would allow users to extend the graphical "syntax" by adding new types that may, or may not, be derived from the Classic object types. Likewise, an Accord layer could closely imitate GrIT and edit conceptual graphs to be processed by PEIRCE.
The Accord approach is potentially useful for knowledge acquisition and knowledge base development. An advantage of using the Accord approach instead of KDraw and GrIT is that users could start very informally, constructing a (non-computational) "knowledge base" without having to commit to a particular knowledge representation, and without the cognitive overhead of having to translate "natural" knowledge into any particular knowledge representation format. As the informal knowledge is built up, its structure may become more obvious. At some point, users may choose an appropriate semantic layer (such as KDraw-like or GrIT-like). Users could then begin to gradually coerce the concept maps to conform to the ontology of the semantic system. Parts of the original concept map may never be converted, but these may safely remain in the system to act as documentation (perhaps as "the road not taken"). In this way, Accord may be developed into a tool which is useful for individuals or groups to record and manipulate ideas and their relationships in a "brainstorming" fashion. This is useful in itself, but if the knowledge turns out to warrant formalization, the tool could also facilitate formalizing this recorded knowledge into a computational knowledge base using a variety of knowledge representation techniques.
The argument has been presented that the users of computer supported concept mapping tools require flexible and forgiving (informal) concept maps, yet the natural services afforded by computer support require typed (formal) concept maps with a formal semantics. The full power of computer supported concept mapping will not be realized unless this dichotomy is addressed.
Concept mapping systems must cleanly support both informal and formal concept mapping simultaneously, and the system should support the transformation from informality to formality with minimal effort on the users part. This is not to say that the system must infer all node and link typing information -- this burden can be shifted to the user by supporting a flexible and extendible typing system on the concept map objects.
Of particular interest is the possibility of using informal concept
mapping tool as a knowledge acquisition technique, then using
the same tool to gradually formalize the informal knowledge into
a computational knowledge base.
1. J. H. Boose, J. M. Bradshaw. "Expertise Transfer and Complex Problems: Using AQUINAS as a Knowledge-Acquisition Workbench for Knowledge-Based Systems." International Journal of Man-Machine Studies, 26(1), 1987, pp. 3-28. Also in Knowledge Acquisition and Learning, B. G. Buchanan and D. C. Wilkins (eds.), Morgan Kaufmann Publishers, San Mateo, California, 1993, pp. 240-252.
2. A. Borgida, R. J. Brachman, D. L. McGuiness, L. A. Resnick. "CLASSIC: A Structural Data Model for Objects." Proceeding of 1989 SIGMOD Conference on the Management of Data, New York, ACM Press, pp. 58-67.
3. J. M. Bradshaw, K. M. Ford, J. R. Adams-Webber, J. H. Boose. "Beyond the Repertory Grid: New Approaches to Constructivist Knowledge Acquisition Tool Development." International Journal of Intelligent Systems, 8, February, 1993.
4. J. Conklin, M. L. Begeman. "gIBIS: A Hypertext Tool for Team Design Deliberation." Hypertext'87, November, 1987, pp. 247-251.
5. P. W. Eklund, J. Leane, C. Nowak. "GRIP: Toward a Standard GUI for Conceptual Structures." Proceedings of the Second International Workshop on PEIRCE: A Conceptual Graphs Workbench, Laval University, Quebec, Canada, August 7, 1993.
6. G. Ellis, R. Levinson, eds. Proceedings of the First International Workshop on PEIRCE: A Conceptual Graphs Workbench, Las Cruccs, New Mexico, 1992.
7. B. R. Gaines. "An Interactive Visual Language for Term Subsumption Languages." Proceedings of IJCAI-91, Sydney, Australia, August 24-30, 1991.
8. B. R. Gaines, M. L. Shaw. "Using Knowledge Acquisition and Representation Tools to Support Scientific Communities." AAAI'94 Conference Proceedings, Seattle, Washington, July, 1994.
9. R. Kremer. "A Concept Map Based Approach to the Shared Workspace." MSc. Thesis, University of Calgary, Canada, June, 1993.
10. J. G. Lambiotte, D. F. Dansereau, D. R. Cross, S. B. Reynolds. "Multirelational Semantic Maps." Educational Psychology Review, 1(4), 1984, pp. 331-367.
11. D. Leishman. "A Principled Analogical Tool Based on Evaluations of Partial Correspondences over Concept Graphs." MSc Thesis, University of Calgary, 1989.
12. J.T. Nosek, I. Roth. "A Comparison of Formal Knowledge Representation Schemes as Communication Tools: Predicate Logic vs. Semantic Network." International Journal of Man-Machine Studies, 33, 1990. pp. 227-239.
13. J. D. Novak, D. B. Gowin, G. T. Johansen. "The Use of Concept Mapping and Knowledge Tree Mapping with Junior high school Science Students." Scientific Education, 67, pp. 625-645.
14. J. F. Nunamaker, A. R. Dennis, J. S. Vaslacich, D. R. Vogel, J.F. George. "Electronic Meeting Systems to Support Group Work." Communications of the ACM, 34(7), July, 1991.
15. M. L. G. Shaw, B. R. Gaines. "A Methodology for Analyzing Terminological and Conceptual Differences in Language Use Across Communities." Proceedings of the First Quantitative Linguistics Conference, QUALICO, Trier, Germany, September 23-27, 1991.
16. P. Smolensky, B. Bell, B. Fox, R. King, C. Lewis. "Constraint-based hypertext for Argumentation." Proceedings of Hypertext'87, New York, ACM, 1987. pp. 215-245.
17. J. F. Sowa. Conceptual Structures:
Information Processing in Mind and Machine. Addison-Wesley,
Reading, Massachusetts, 1984.